The speed of river current close to banks is nearly zero. The current speed increases linearly from the banks to become maximum (=V0) in the middle of the river. A boat has speed ‘u’ in still water. It starts from one bank and crosses the river. Its velocity relative to water is always kept perpendicular to the current. Find the distance through which the boat will get carried away by the current (along the direction of flow) while it crosses the river. Width of the river is l.
The correct Answer is:V0l2u
Step by step video, text & image solution for The speed of river current close to banks is nearly zero. The current speed increases linearly from the banks to become maximum (= V_(0)) in the middle of the river. A boat has speed ‘u’ in still water. It starts from one bank and crosses the river. Its velocity relative to water is always kept perpendicular to the current. Find the distance through which the boat will get carried away by the current (along the direction of flow) while it crosses the river. Width of the river is l. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The current velocity of river grows in proportion to the distance from its bank and reaches the maximum value v0 in the middle. Near the banks the velocity is zero. A boat is moving along the river in such a manner that the boatman rows his boat always perpendicular to the current. The speed of the boat in still water is u. Find the distance through which the boat crossing the river will be carried away by the current, if the width of the river is c. Also determine the trajectory of the boat.
View SolutionWhen a sailor jumps from a boat to the river bank?
View Solution
Knowledge Check
A man swims to and fro along the bank of a river with a velocity v relative to water. If the velocity of flow is u, the average speed of the man (for to and fro motion) is :
A0B√uvCu+v2Dv2−u2vA man who can swim at a velocity v relative to water wants to cross a river of width b, flowing with a speed u.
AThe minimum time in which he can cross the river is bvBHe can reach a point exactly opposite on the bank in time t=b√v2−u2ifv>uCHe cannot reach a point exactly opposite on the bank if u>vDHe cannot reach a point exactly opposite on the bank if v>uThe speed of boat is 5kmh−1 in still water. It crosses a river of width 1 km along the shortest possible path in 15 min. Then, velocity of river will be
A3 km/hrB4 km/hrC5 km/hrD2 km/hr
The speed of a swimmer with respect to the water is v, the speed of the stream is u. In what direction should the swimmer move to reach the opposite point on the other bank of the river? How long will he swim if the width of the river is l?
View SolutionA person rows a boat in a water with a speed of 4ms−1. Water in the river is flowing with a speed of 2ms−1 . If the person rows the boat perpendiculat to thedirection of flow, find resultant velcity of the boat and time taken by boat to cross the river if widthe of the river is 400m.
View SolutionA boat crossing a river moves with a velocity v relative to still water. The river is flowing with a velocity v/2 with respect to the bank. The angle with respect to the flow direction with which the boat should move to minimize the drift is–
View SolutionThe width of a river is 2√3km.A boat is rowed in direction perpendicular to the banks of river.If the drift of the boat due to flow is 2km,the displacement of the boat is.
View Solution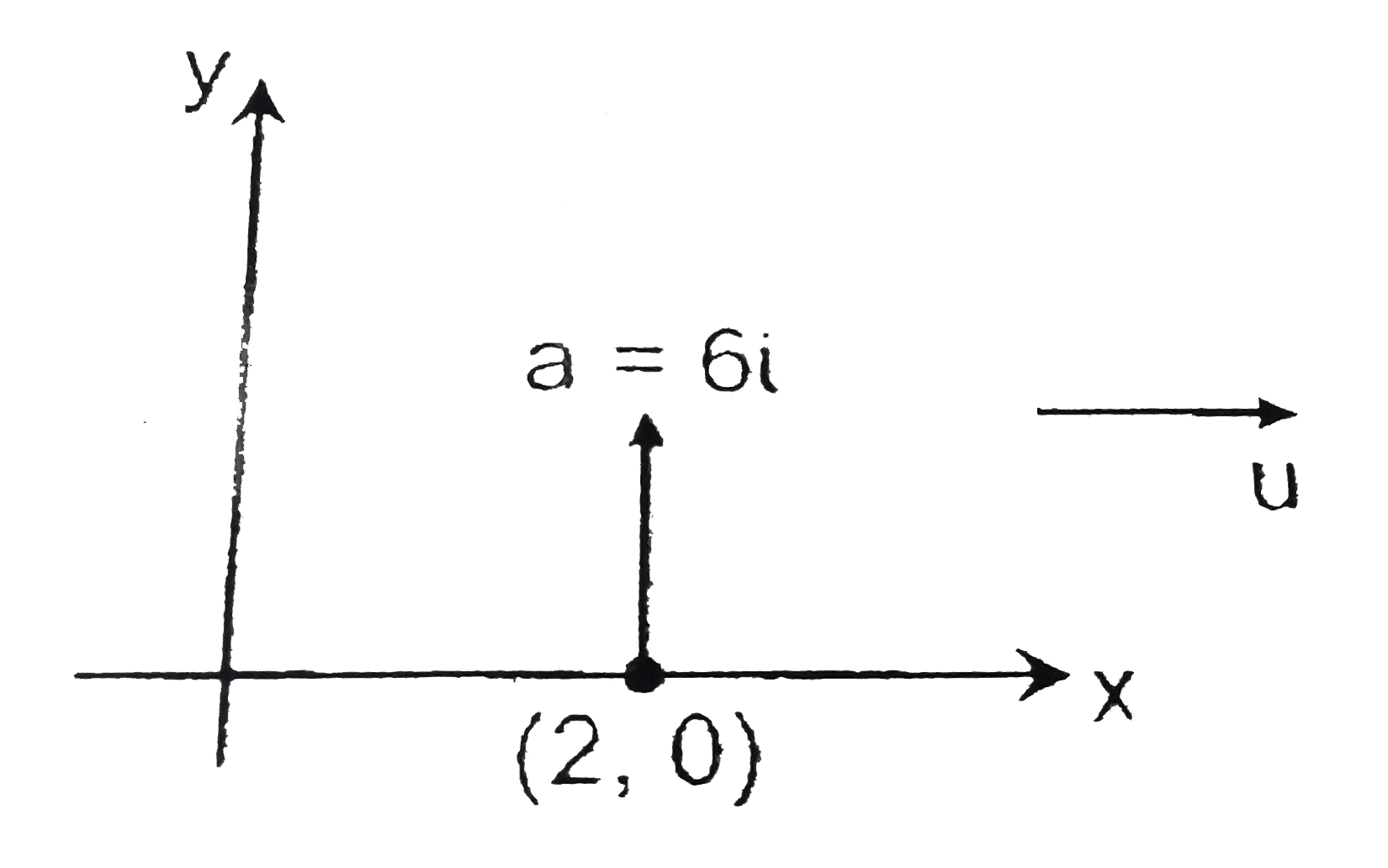
A boat starting from rest aims perpendicular to the river with an acceleration of a=6t
(where t= time) the boat starts from (2,0) of the coordinate system. Find equation of trajectory. Given velocity of river =u.
View Solution

