
A particle is moving in x–y plane. The x and y components of its acceleration change with time according to the graphs given in figure. At time t=0, its velocity is v0 directed along positive y direction. if a0=v0t0, find the angle that the velocity of the particle makes with x axis at time t=4t0.
The correct Answer is:θ=tam−1(32)
Step by step video, text & image solution for A particle is moving in x–y plane. The x and y components of its acceleration change with time according to the graphs given in figure. At time t = 0, its velocity is v_(0) directed along positive y direction. if a_(0) = (v_(0))/(t_(0)), find the angle that the velocity of the particle makes with x axis at time t = 4t_(0). by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICSBook:ARIHANTChapter:KINEMATICSExercise:Level 3
Explore 33 Videos
- KINEMATICSBook:ARIHANTChapter:KINEMATICSExercise:Level 3
Explore 33 Videos
- HEAT TRANSFERBook:ARIHANTChapter:HEAT TRANSFERExercise:Heat Transfer
Explore 45 Videos
- KINETIC THEORY OF GASESBook:ARIHANTChapter:KINETIC THEORY OF GASESExercise:Level 3
Explore 4 Videos
Similar Questions
A particle moves vertically with an upward initial speed v0=5m/s. If its acceleration varies with time as shwon in a−t graph in the fig. 4.30, find the velocity of the particle at t=7s.

View SolutionA particle moves vertically with an upwards initial speed v0=10.5ms−1. If its acceleration varies with time as shown in a-t graph in figure, find the velocity of the particles at t = 4s.

View Solution
Knowledge Check
An object is moving in x−y plane its velocity and acceleration at t=0 are represented in figure.

After how much time object crosses the y−axis:-A4secB2secC3secDNoneA particle moves along x axis in such a way that its coordinate x varies with time t according to the equation x=A0−A1t+A2t2. The initial velocity of the particle is.
AA0BA1CA2D−A1A particle is moving in a straight line whose acceleration versus time graph is given. Assume that initial velocity is in the direction of acceleration. Then
which of the statement is correct between time t=0 to t=t0.
 .AVelocity first increases then decreases, displacement always increasesBVelocity and displacement both, first increases and then decreasesCDisplacement increases and velocity decreasesDDisplacement and velocity both always increases.
.AVelocity first increases then decreases, displacement always increasesBVelocity and displacement both, first increases and then decreasesCDisplacement increases and velocity decreasesDDisplacement and velocity both always increases.
A particle is moving along positive x direction and experiences a constant acceleration of 4m/s2 in negative x direction. At time t=3 second its velocity was observed to be 10m/s in positive x direction.
(a) Find the distance travelled by the particle in the interval t=0 to t=3s. Also find distance travelled in the interval t=0 to t=7.5s..
(b) Plot the displacement – time graph for the interval t=0 to 7.5s.
View SolutionThe magnitude of force acting on a particle moving along x-axis varies with time (t) as shown in figure. If at t = 0 the velocity of particle is v0, then its velocity at t=T0 will be

View SolutionA particle is moving in a straight line according to graph given below : (a is acceleration, v is velocity, x is position, t is time) :
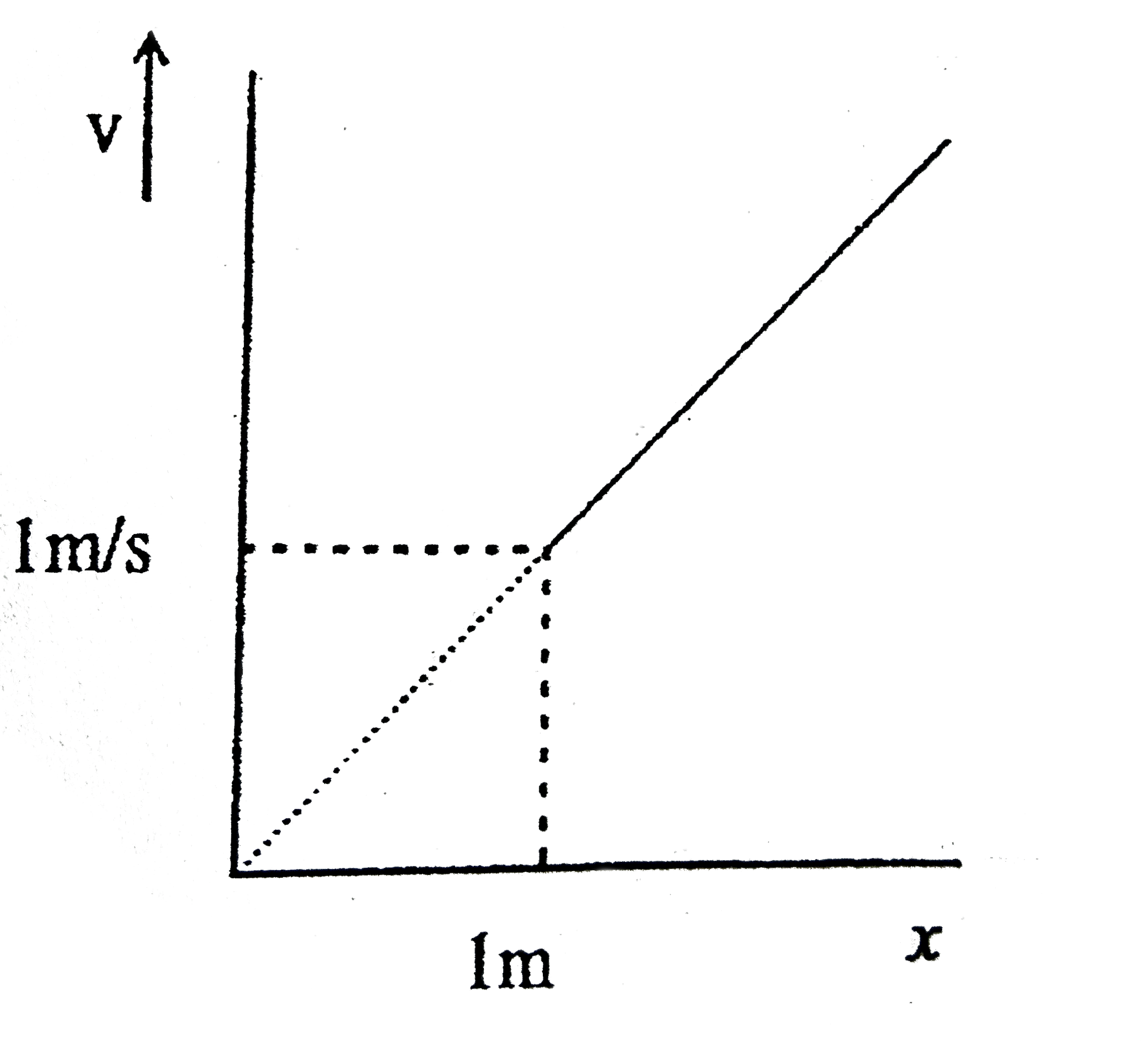
View SolutionFor the acceleration - time (a - t) graph shown in figure, the change in velocity of particle from t = 0 to t = 6 s is
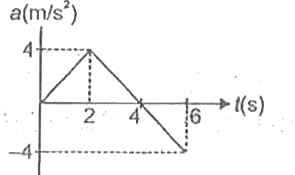
View SolutionA particle located at x=0 at time t=0, starts moving along with the positive x−direction with a velocity 'v' that varies as v=a√x. The displacement of the particle varies with time as
View Solution

