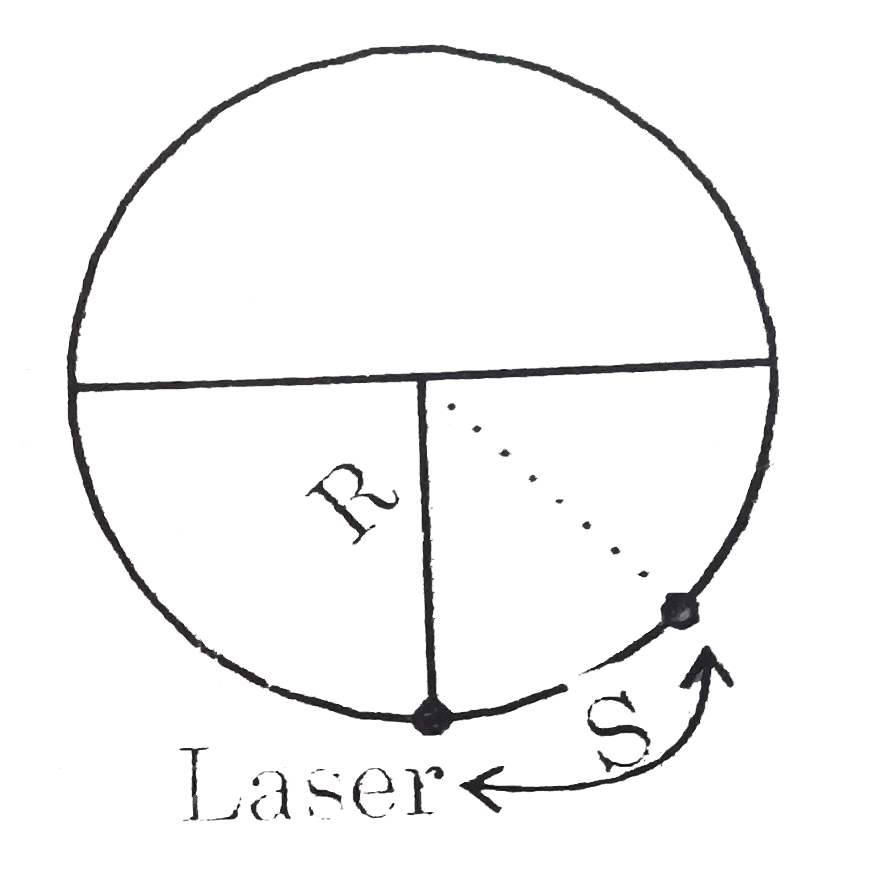
A horizontal cylinderical tank 6πm in diameter is half full of water. The space above the water is filled with a pressurized gas of unknown refractive index. A small laser can move along the curved bottom of the water and aims a light beam towards the centre of the water surface. When the laser has moved a distance s=1m or more (measured from curved face) from the lowest point in water, no light enters the gas. The refractive index of gas is (μwater=4/3)
4/√3
√5/2
2/√3
√3
The correct Answer is:C
Distance moved by laser S=Rθ
θ=SR=π3rad
If s>1m when no light enetrs the gas critical angle c=θ
⇒1sin60=μWμG=2√3∴μ=2√3
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PHYSICS
18 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - MATHS
18 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - part-2 physics
63 Videos
- TEST PAPER 4BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS
45 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
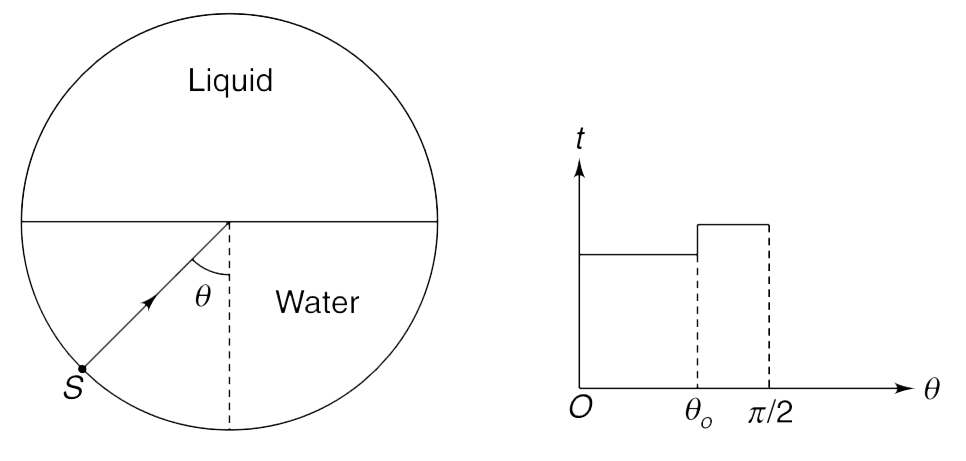
A horizontal cylindrical tank is half full of water ( refractive index =43) . The space above the water is filled with a light liquid of unknown refractive index (μ). A small laser source (s) can move along the curved bottom of the cylinder and aims a light beam towards the centre of the cylinder. The time needed by the laser beam to travel from the source to the rim of the cylinder depends on position (θ) of the source as shown in the graph. Find μ, it is given that sinθ0=56.
View SolutionA cylinderical bucket 28 cm in diameter and 72 cm high is full of water . The water is emptied in to a rectangualr tank 66 cm long and 28 cm wide .Find the height of water level in the tank.
View Solution
Knowledge Check
A cylindrical tank of diameter 35 cm is full of water. If 11 litres of water is drawn off, the water level in the tank will drop by :
(use π=227)A1012cmB1267cmC14 cmD1137cmA point source of light is placed at a depth of h below the surface of water of refractive index μ.A floating opaque disc is placed on the surface of water so that light from the source is not visible from the surface . The minimum diameter of the disc is
A2h(μ2−1)12B2h(μ2−1)12Ch2(μ2−1)12Dh(μ2−1)12A point source of light is placed at a depth of h below the surface of water of refractive index μ. A floating opaque disc is placed on the surface of water so that light from the source is not visible from the surface. The minimum diameter of the disc is
A2h(μ2−1)1/2B2h(μ2−1)1/2Ch2(μ2−1)1/2Dh(μ2−1)1/2
In a tank filled with a liquid of refractive index 5/3, a point source of light is placed 2m below the surface of water. To cut off all light coming out of water from the source, what should be the minimum diameter of a disc, which should be placed over the source on the surface of water ?
View SolutionA rectangular tank 8m deep is full of water. By how much does the bottom appear to be raised if the refractive index of water is 4/3?
View SolutionA point source is placed at a depth h below the surface of water (refractive index =μ). The medium above the surface of water is air from water.
View SolutionIf the refractive index from air to glass is 1.5 ,and the refractive index of water is 1.33. What is the refractive index from glass into water?
View SolutionA jet of water issunig from a hole mear the bottom of water tank is an…………………………. .
View Solution
