In a continuous printing process paper is drawn into the press at a constant speed v. Denoting by 'r' the radius of the paper roll at any given time and by 'b' the thickness of the paper. What is the angular acceleraion of the paper roll? 
bv22πr3
2bv2πr3
bv24πr3
4bv2πr3
The correct Answer is:A
Let one layer of paper be unrolled
vΔt=2πrandΔr=−b
ΔrΔt=−bv2πr=drdt
α=dωdt=ddt(vr)
=1rdvdt+vddt(1r)
=0−vr2drdt
=(−vr2)(−bv2πr)
bv22πr3
α=bv22πr3
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PHYSICS
18 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - MATHS
18 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - part-2 physics
63 Videos
- TEST PAPER 4BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS
45 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
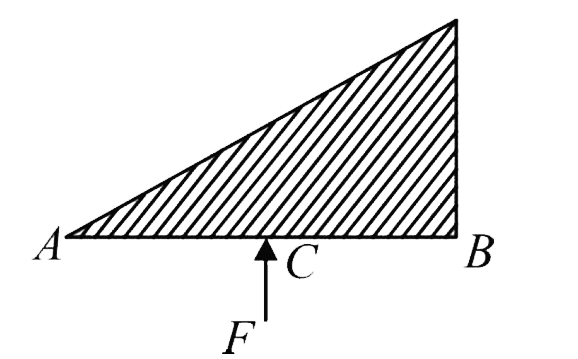
A triangular plate of uniform thickness and density is made to rotate about an axis perpendicular to the plane of the paper and (a) passing through A,(b) passing through B, by the application of the same force, F, at C (midpoint of AB) as shown in the figure. The angular acceleration in both the cases will be the same.
View SolutionA square sheet of paper is converted into a cylinder by rolling it along its side.What is the ratio of the base radius to the side of the square?
View Solution
Knowledge Check
Density of the material of a paper is given a 0.5 g cm−3. The mass of the paper is 1 g and its length and breadth are 10 c and 5 cm, respectively. Arrange the following steps in a sequence to find the thickness of the paper.
(A). The 0thickness of the paper is Volume of the paper (m)Vlume of the paper (V)
(B) The density (d) of the material of the paper is =Mass of the paper (m)volume of the paper (V)
(C). then the volume (V) o the paper
=Mass of the paper (m)Density (d) of the paper
(D). The volume (V) of the paper is=length×breadth×thickness of the paper.AABCDBBADCCABDCDBCDAA disc of the radius R is confined to roll without slipping at A and B. If the plates have the velocities v and 2v as shown, the angular velocity of the disc is
 A3V2R AnticlockwiseB3V2R ClockwiseCV2R AnticlockwiseDV2R clockwise
A3V2R AnticlockwiseB3V2R ClockwiseCV2R AnticlockwiseDV2R clockwiseA sphere of mass M rolls without slipping on rough surface with centre of mass has constant speed v0. If mass of the sphere is m and its radius be R, then the angular momentum of the sphere about the point of contact is.
A45Mv0R(−ˆk)B95Mv0R(−ˆk)C85Mv0R(−ˆk)D75Mv0R(−ˆk)
A rectangular sheat of paper 44cm x 18cm is rolled along its length and a cylinder is formed. Find the radius of the cylinder.
View SolutionA rectangular sheet of paper 44cm×18cm is rolled along its length and a cylinder is formed. Find the radius of the cylinder.
View SolutionA rectangular sheat of paper 44cm x 18cm is rolled along its length and a cylinder is formed. Find the radius of the cylinder.
View SolutionA rectangular paper of 44 cm long and 6 cm wide is rolled to form a cylinder of height equal to width of the paper. The radius of the base of the cylinder so rolled is
View SolutionA ring of radius R is rolling purely on the outer surface of a pipe of radius 4R At some instant the center of the ring has constant speed =v then the acceleration of the point on the ring which is in contact with the surface of the pipe is
View Solution
