If a slab of insulating material4×10–5m thick is introduced between the plates of a parallel plate capacitor, the distance between the plates has to be increased by 3.5×10–5 m to restore the capacity to original value. Then the dielectric constant of the material of slab is
8
6
12
10
To solve the problem, we need to find the dielectric constant k of the insulating slab introduced between the plates of a parallel plate capacitor. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Initial Capacitance
The initial capacitance C of a parallel plate capacitor without the dielectric is given by:
C=Aϵ0d
where:
- A is the area of the plates,
- ϵ0 is the permittivity of free space,
- d is the separation between the plates.
Step 2: Introduce the Dielectric Slab
When a dielectric slab of thickness t=4×10−5m is introduced, the effective capacitance changes. The new distance between the plates after introducing the slab and increasing the distance by d1=3.5×10−5m becomes:
d′=d+d1
Thus, the new distance d′ is:
d′=d+3.5×10−5
Step 3: Calculate the New Capacitance
The new capacitance C′ can be calculated using the formula for capacitors in series. The capacitor can be thought of as two capacitors in series: one with the dielectric and one with air. The capacitance of the part with the dielectric is:
C1=Aϵ0d′−t
And the capacitance of the part with air is:
C2=Aϵ0d′
The equivalent capacitance Ceq is given by:
1Ceq=1C1+1C2
Step 4: Set the Capacitance Equal to the Original
To restore the capacitance to its original value, we set Ceq=C:
1C=1C1+1C2
Substituting the expressions for C1 and C2:
1Aϵ0d=1Aϵ0d′−t+1Aϵ0d′
This simplifies to:
d′Aϵ0=d′−tAϵ0+d′Aϵ0
Step 5: Solve for the Dielectric Constant
After simplifying and rearranging, we find:
d′−d=t−tk
Substituting t=4×10−5 and d′−d=3.5×10−5:
3.5×10−5=4×10−5−4×10−5k
Rearranging gives:
4×10−5k=4×10−5−3.5×10−5
4×10−5k=0.5×10−5
Thus:
k=4×10−50.5×10−5=8
Final Answer
The dielectric constant k of the material of the slab is:
8
The initial capacitance C of a parallel plate capacitor without the dielectric is given by:
C=Aϵ0d
where:
- A is the area of the plates,
- ϵ0 is the permittivity of free space,
- d is the separation between the plates.
When a dielectric slab of thickness t=4×10−5m is introduced, the effective capacitance changes. The new distance between the plates after introducing the slab and increasing the distance by d1=3.5×10−5m becomes:
d′=d+d1
Thus, the new distance d′ is:
d′=d+3.5×10−5
The new capacitance C′ can be calculated using the formula for capacitors in series. The capacitor can be thought of as two capacitors in series: one with the dielectric and one with air. The capacitance of the part with the dielectric is:
C1=Aϵ0d′−t
And the capacitance of the part with air is:
C2=Aϵ0d′
The equivalent capacitance Ceq is given by:
1Ceq=1C1+1C2
To restore the capacitance to its original value, we set Ceq=C:
1C=1C1+1C2
Substituting the expressions for C1 and C2:
1Aϵ0d=1Aϵ0d′−t+1Aϵ0d′
This simplifies to:
d′Aϵ0=d′−tAϵ0+d′Aϵ0
After simplifying and rearranging, we find:
d′−d=t−tk
Substituting t=4×10−5 and d′−d=3.5×10−5:
3.5×10−5=4×10−5−4×10−5k
Rearranging gives:
4×10−5k=4×10−5−3.5×10−5
4×10−5k=0.5×10−5
Thus:
k=4×10−50.5×10−5=8
The dielectric constant k of the material of the slab is:
8
Topper's Solved these Questions
Similar Questions
When a slab of inslulating material 4mm thick is inroduced between the plates of a parallel plate capacitor, it is found that the distance between the plates has to be increased by 3.2mm to restore the capacity to its original value. Calculate dielectric constant of the material.
View SolutionAn ebomiote rod (K = 3), 6 mm thick is introduced between the plates of a parallel plate capacitor of plate area 4×10−2m2 and plate separation 0.01m. Find the capacitance.
View Solution
Knowledge Check
When a dielectric slab of thickness 4cm is introduced between the plates of parallel plate condenser, it is found the distance between the plates has to be increased by 3cm to restore to capacity to original value. The dielectric constant of the slab is.
A1//4B4C3D1When a dielectric slab of thickness 4cm is introduced between the plates of parallel plate condenser, it is found the distance between the plates has to be increased by 3cm to restore to capacity to original value. The dielectric constant of the slab is.
A1/4B4C3D1A dielectric slab is placed between the plates of a parallel plate capacitor. Its capacitance
Abecomes zeroBremains the sameCdecreasesDincreases
A metal slab of thickness, equal to half the distance between the plates is introduced between the plates of a parallel plate capacitor as shown. Find its capacity.
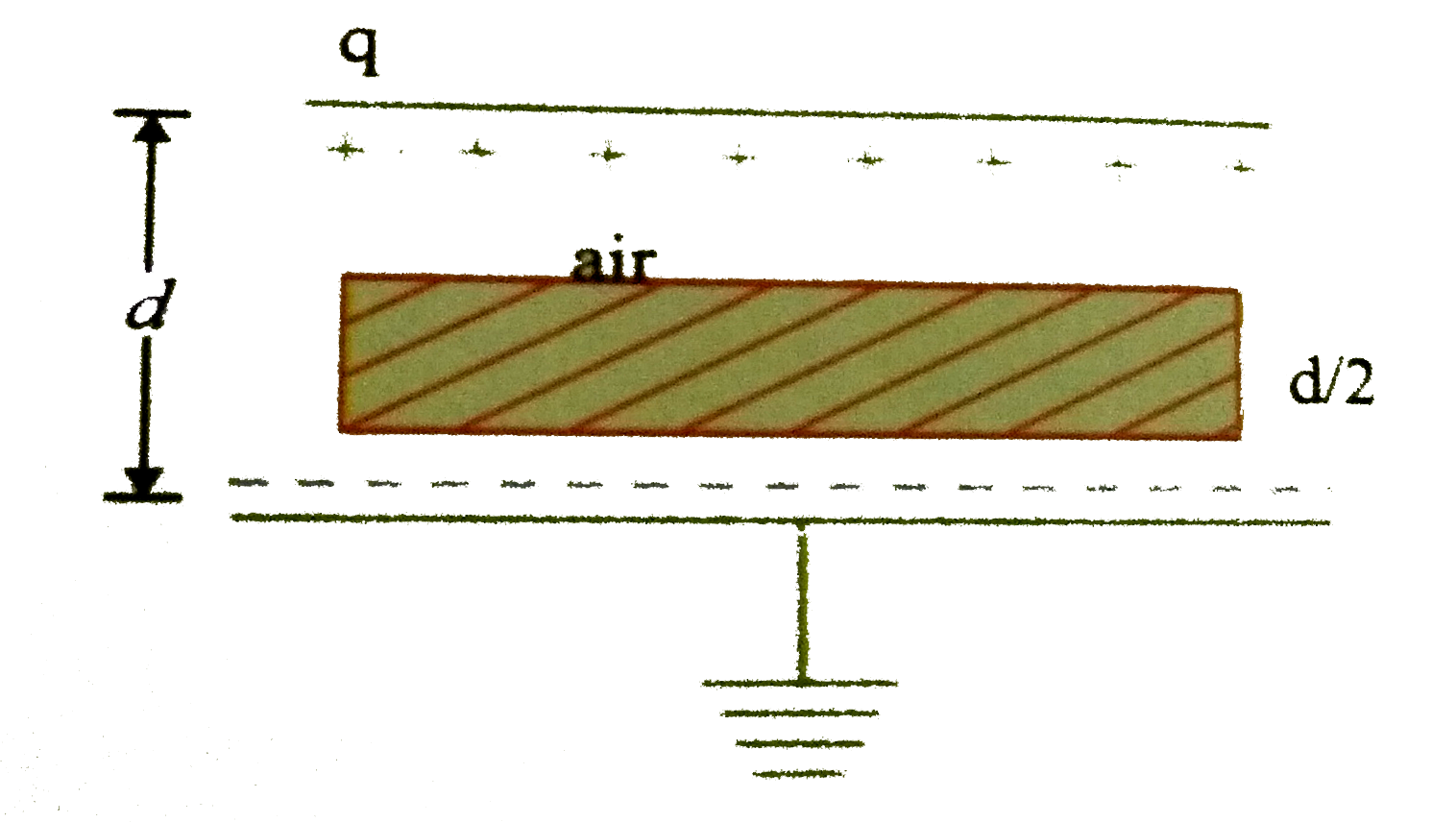 .
.
View SolutionThe two plates of a parallel plate capacitor are 4 mm apart . A slab of dielectric constant 3 and thickness 3 mm is introduced between the plates with its face parallel to them . The distance between the plates is so adjusted that the capacity of the capacitor becomes 23 rd of its original value . What is the new distance the plates ?
View SolutionExplain why the capacitance of a parallel plate capacitor increases when a dielectric slab is introduced between the plates.
View SolutionA dielectric slab of thickness 't' is kept between the plates of a parallel plate capacitor separated by a distance 'd' (t<d) . Derive the expression for the capacity of the capacitor .
View SolutionIf a dielectric slab of thickness 5 mm and dielectric constant K=6 is introduced between the plates of a parallel plate air capacitor, with plate separation of 8 mm, then its capacitance is
View Solution
