A vector of magnitude b is rotated through angle θ. What is the change in magnitude of the vector?
2bsinθ2
2bcosθ2
2bsinθ
2bcosθ
To solve the problem of finding the change in magnitude of a vector of magnitude b when it is rotated through an angle θ, we can follow these steps:
1. Understanding the Problem:
We have a vector →v with an initial magnitude b. When this vector is rotated through an angle θ, we need to find the change in its magnitude.
2. Initial and Final Vectors:
Let the initial vector be →v with magnitude b. After rotation, let the new vector be →v′.
3. Using the Law of Cosines:
When the vector is rotated, the change in the vector can be represented as:
→v′=→v+→u
where →u is the displacement vector due to the rotation. The magnitude of →u can be found using the law of cosines:
|→u|=|→v′−→v|=√|→v′|2+|→v|2−2|→v′||→v|cos(θ)
4. Magnitude of the New Vector:
Since both vectors →v and →v′ have the same magnitude b, we can substitute:
|→u|=√b2+b2−2b2cos(θ)=√2b2(1−cos(θ))
5. Simplifying the Expression:
This simplifies to:
|→u|=b√2(1−cos(θ))
6. Using the Identity:
We can use the trigonometric identity 1−cos(θ)=2sin2(θ2):
|→u|=b√2⋅2sin2(θ2)=2bsin(θ2)
7. Final Change in Magnitude:
The change in magnitude of the vector when it is rotated through angle θ is:
Δb=|→u|=2bsin(θ2)
Conclusion:
The change in magnitude of the vector when it is rotated through an angle θ is given by:
Δb=2bsin(θ2)
We have a vector →v with an initial magnitude b. When this vector is rotated through an angle θ, we need to find the change in its magnitude.
Let the initial vector be →v with magnitude b. After rotation, let the new vector be →v′.
When the vector is rotated, the change in the vector can be represented as:
→v′=→v+→u
where →u is the displacement vector due to the rotation. The magnitude of →u can be found using the law of cosines:
|→u|=|→v′−→v|=√|→v′|2+|→v|2−2|→v′||→v|cos(θ)
Since both vectors →v and →v′ have the same magnitude b, we can substitute:
|→u|=√b2+b2−2b2cos(θ)=√2b2(1−cos(θ))
This simplifies to:
|→u|=b√2(1−cos(θ))
We can use the trigonometric identity 1−cos(θ)=2sin2(θ2):
|→u|=b√2⋅2sin2(θ2)=2bsin(θ2)
The change in magnitude of the vector when it is rotated through angle θ is:
Δb=|→u|=2bsin(θ2)
The change in magnitude of the vector when it is rotated through an angle θ is given by:
Δb=2bsin(θ2)
Topper's Solved these Questions
Similar Questions
Knowledge Check
A vector of magnitude a is turned through angle θ . The magnitude of change in the vector is given by:
A|2asinθ|B|2asinθ/2|C∣∣∣a2sinθ∣∣∣D∣∣∣a2sinθ/2∣∣∣A vector of length l is turned through the angle θ about its tail. What is the change in the position vector of its head ?
Alcos(θ/2)B2lsin(θ/2)C2lcos(θ/2)Dlsin(θ/2)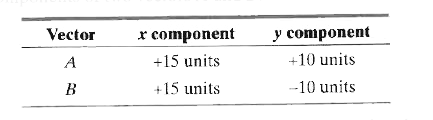
Determine the magnitude of the vector sum, A+B.A5 unitsB15 unitsC20 unitsD30 units
The vector ˆi+xˆj+3ˆk is rotated through an angle θ and doubled in magnitude then it becomes 4ˆi+(4x−2)ˆj+2ˆk.The values of x
View SolutionA vector →A is rotated through angle θ about its tail. Change of position vector of its tip of is:
View SolutionIf →A is a vector of magnitude 3 units due east. What is the magnitude and direction of a vector −4→A ?
View SolutionIf →A is a vector of magnitudes 5units due east. What is the magnitude and direction of a vector −5→A?
View SolutionThe vector ˆi+xˆj+3ˆk is rotated through an angle θ and doubled in magnitude, then it becomes 4ˆi+(4x−2)ˆi+2ˆk. The value of x is
View Solution