Prove that the cosine formula for triangles is equivalent to the definition of the scalar product.
Video Solution
Text Solution
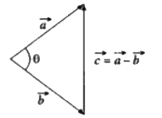
Let two sides of a triangle represent the two vectors →aand→b .
Then the third side is →c=→a−→b
(→a−→b).(→a−→b)=→c.→c
a2−→a.→b−→b−→a+b2=c2
a2+b2−2→a.→b=c2
→a.→b=abcosθ
where θ is the angle between the two vectors →aand→b .
This is the cosine law .
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The equivalent definition of the function given by
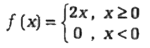 isAf(x)=|x|Bf(x)=2xCf(x)=|x|+xDf(x)=2|x|
isAf(x)=|x|Bf(x)=2xCf(x)=|x|+xDf(x)=2|x|The equivalent definition of f(x)=||x|−1|, is
Af(x)=⎧⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪⎩−x−1x≤−1x+1−1<x≤01−x0≤x≤1x−1x≤1Bf(x)=⎧⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪⎩x−1x≤−1x+1−1<x≤0x−10≤x≤1x+1x≥1Cf(x)={x+1x≥0x+1x≤0Dnone of theseDimensional formula for Joule's mechanical equivalent is
A[M−1L−3T4A2]B[M0L0T0A0]C[M−1LTA−1]D[M−1L−1T4]
cosine law OF triangle
View SolutionScalar Triple Product
View SolutionIf a triangle is inscribed in a circle, then prove that the product of any two sides of the triangle is equal to the product of the diameter and the perpendicular distance of the thrid side from the opposite vertex.
View SolutionDefinition and meaning of cross product
View SolutionScalar Triple Product |
View Solution

