For any vector →a and →b prove that ∣∣→a+→b∣∣≤|→a|+∣∣→b∣∣.
Video Solution
Text Solution
Let OA=a and AB=b. completing the parallelogram OABC.
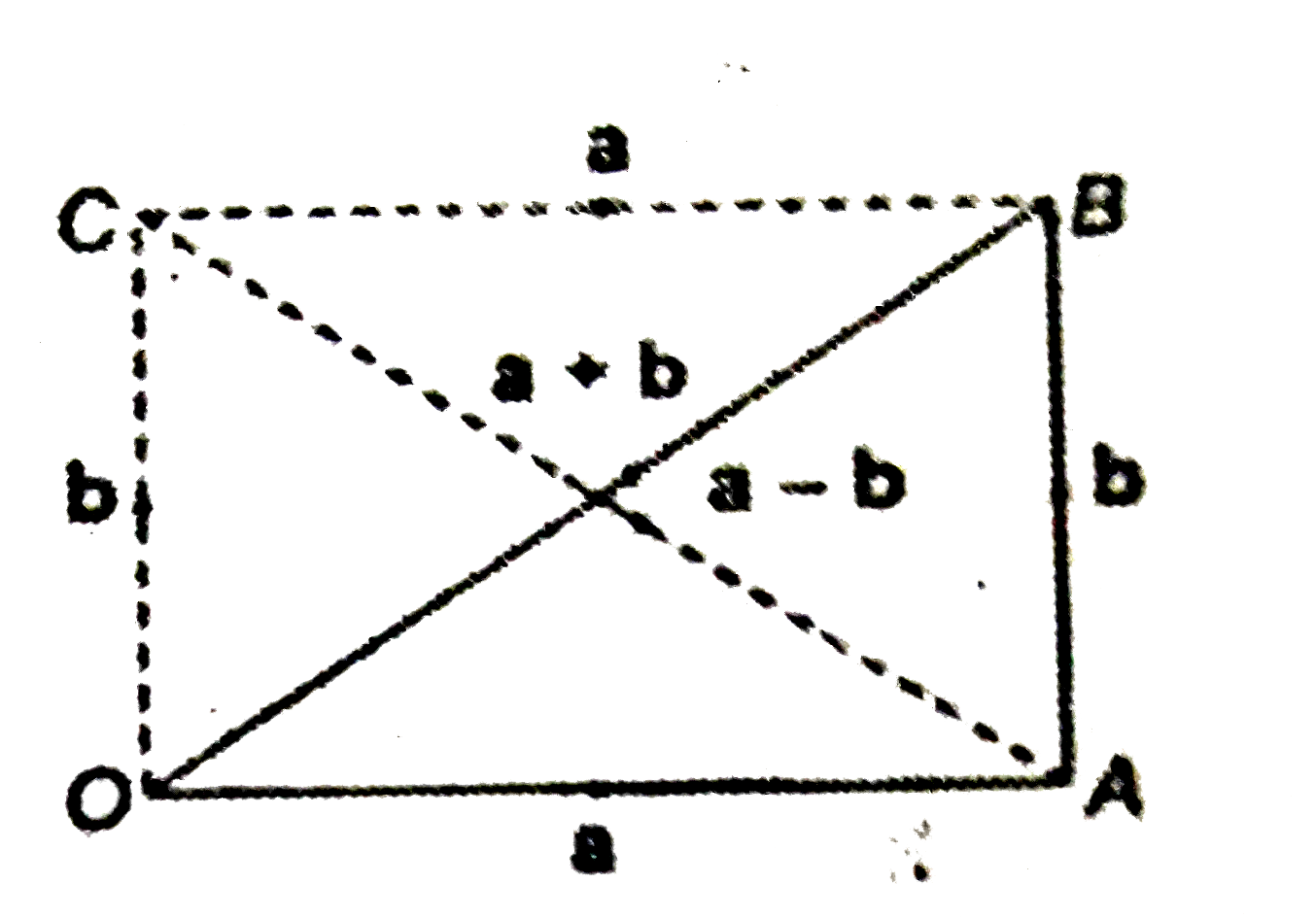
Then, OC=b and CB=a
from ΔOAB, we have
OA+AB=Ob⇒a+b=OB . . . (i)
From ΔOCA, we have
OC+CA=OA
⇒b+CA=a⇒CA=a−b . . . (ii)
Clearly, |a+b|=|a−b|⇒|OB|=|CA|
Diagonals of parallelogram OABC are qual.
OABC is a rectangle.
⇒OA⊥OC⇒a⊥b.
|
Similar Questions
For any two vectors →aand→b prove that ∣∣→a+→b∣∣≤|→a|+∣∣→b∣∣
View SolutionFor any two vectors →aand→b , prove that ∣∣→a+→b∣∣≤|→a|+∣∣→b∣∣
View SolutionFor any vector →a and →b prove that ∣∣→a+→b∣∣≤|→a|+∣∣→b∣∣.
View SolutionFor any two vectors →a and →b , prove that (→a×→b)2=|→a|2∣∣→b∣∣2−(→a.→b)2
View Solutionfor any two vectors →aand→b, show that ∣∣→a.→b∣∣≤|→a|∣∣→b∣∣
View SolutionFor any two vectors →a and →b write when ∣∣→a+→b∣∣=|→a|+∣∣→b∣∣ holds.
View SolutionFor any two vectors →a and →b, we always have ∣∣→a+→b∣∣≤|→a|+∣∣→b∣∣
View SolutionFor any two vectors →aand→b, prove that ⎛⎜⎝→a|→a|2−→b∣∣→b∣∣2⎞⎟⎠2=⎛⎜⎝→a−→b|→a|∣∣→b∣∣⎞⎟⎠2
View SolutionFor any two vectors →a and →b, fin d\ (→a×→b).→b.
View SolutionFor any two vectors →a and →b write when ∣∣→a+→b∣∣=∣∣→a−→b∣∣ holds.
View Solution
