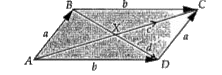
$A B C D$ is a parallelogram with $A C$ and $B D$ as diagonals. Then, $- - \to A C - - - \to B D =$

a) $4 - - \to A B$

b) $3 - - \to A B$

c) $2 - - \to A B$

d) $- - \to A B$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:c) $2 - - \to A B$

Updated on:21/07/2023

ABCD is a parallelogram with AC and BD as diagonals. Then, $A \to C - B \to D =$
A $4 A \to B$
B $3 A \to B$
C $2 A \to B$
D $A \to B$
ABCD is a parallelogram whose adjacent sides are represented by the vectors $\to a$ and $\to b$ . Three of its vertices are A(1,2,3),B(2,0,5) and D(-1,4,1).

The diagonal $\to c =$ _________.
A $ˆ i + 3 ˆ j + 5 ˆ k$
B $ˆ i + ˆ j - ˆ k$
C $- ˆ i$
D $- ˆ j$
If $\to a, \to b, \to c$ are the position vectors of corners A, B, C or a parallelogram ABCD, then what is the position vector of the corner D?
A $\to a + \to b + \to c$
B $\to a + \to b - \to c$
C $\to a - \to b + \to c$
D $- \to a + \to b + \to c$