Question

Let O be an interior point of $\Delta ABC$ such that $\overline{OA}+2\overline{OB}+3\overline{OC}=0$. Then the ratio of a $\Delta ABC$ to area of $\Delta AOC$ is

Answer

3

Explanation

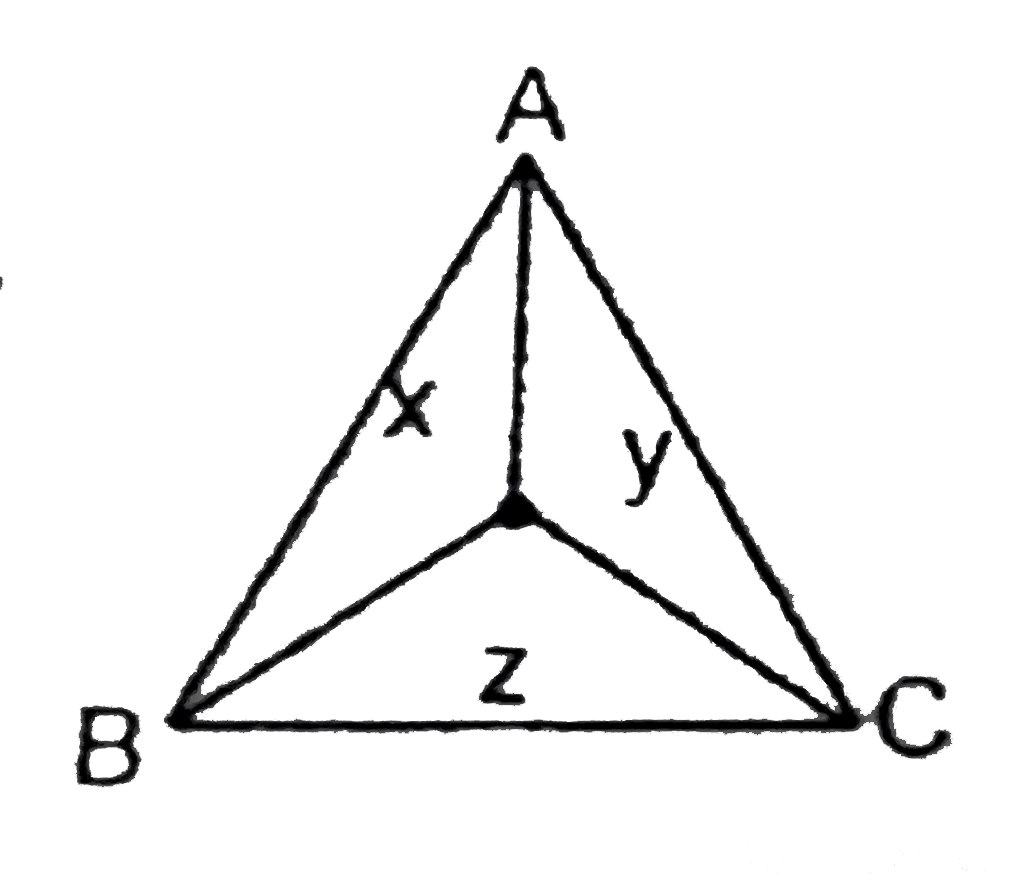
`overline(OA)+overline(2OB)+overline(3OC)=ver0` .(i)
let x,y,z be the area of Delta `OAB,OBC` and `OCA`
respectively and area `(DeltaABC)=A`
`impliesx+y+z=A` .(ii)
Taking cross product with `overline(OA)` on the both sides (i) and then take modulus on both sides. We get
`(x)/(y)=(3)/(2)impliesx+(3)/(2)y`
similarly `(x)/(z)=3` and `(y)/(z)=2impliesz=(y)/(2)`
`because` from (ii) `y((3)/(2)+1+(1)/(2))=Aimplies(A)/(y)=3`