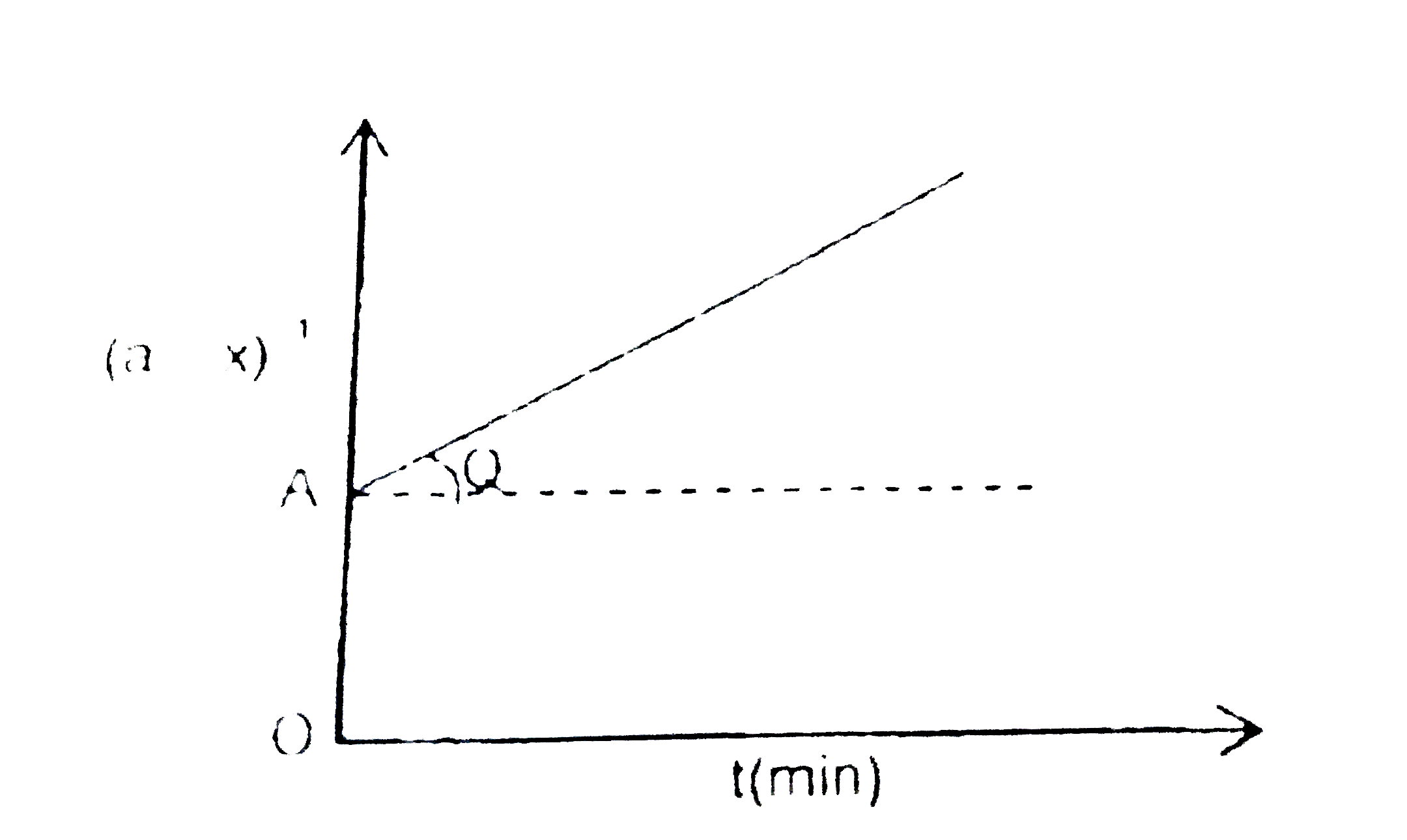
Following is the graph between ${(a - x)}^{- 1}$ and time for second order reaction $A \to 2 B, Q = {tan}^{- 1} (0.5), O A = 2 L m o l^{- 1}$ . Here is the initial concentration of reactant and x is its amount reactedc at any time t. Hence rate at the start of the reaction is:

A

$0.125 L m o l^{- 1} m o l^{- 1}$

B

$0.25 m o l L^{- 1} - 1 min$

C

$0.125 m o l L^{- 1} - 1 min$

D

$0.25 L m o l^{- 1} - 1 min$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

For second order reaction,
$∵ {(a - x)}^{- 1} = \frac{1}{K t} + \frac{I}{a}$
$∵ k = tan θ (∵ tan θ = 0.5$ from question)
$∵ K = 0.5$ lit $m o l^{- 1} - 1 min$
and $\frac{I}{a} = 2$ or $a = 0.5 M$
$r = K a^{2}$
$= 0.5 \times {0.5}^{2}$
$= 0.125 m o l L^{- 1} - 1 min$

|

Updated on:21/07/2023

Class 12 CHEMISTRY TEST PAPERS

Similar Questions

Knowledge Check

Question 1 - Select One
Following is the graph between $(a - x)$ and time $t$ for second order reaction $θ = {tan}^{- 1} (0.5) O A = 2 L m o l^{-}$

Hence, the rate at the start of the reaction is
A $1.25 m o l L^{- 1} m i n^{- 1}$
B $0.5 m o l L^{- 1} m i n^{- 1}$
C $0.125 m o l L^{- 1} m i^{- 1}$
D $12.5 m o l L^{- 1} - 1 min$
Question 2 - Select One
In a reaction the initial concentration of the reactants increase four fold and the rate becomes eight times its initial value . The order of the reaction is
A $2.0$
B $3.5$
C $2.5$
D $1.5$
Question 3 - Select One
when concentration of reactant in reaction $A \to B$ is increased by 4 times , the rate increase only 2 times The order of the reaction would be
A2
B $\frac{1}{3}$
C $4$
D $\frac{1}{2}$

Recommended Questions

Home
Ask Doubt
Profile