→a and →b are two given vectors. On these vectors as adjacent sides a parallelogram is constructed. The vector which is the altitude of the parallelogam and which is perpendicular to →a is not equal to
(→a.→b)|→a|2→a−→b
1|→a|2{|→a|2→b−(→a.→b)→a}
→a×(→a×→b)|→a|2
→a×(→b×→a)∣∣→b∣∣2
The correct Answer is:D
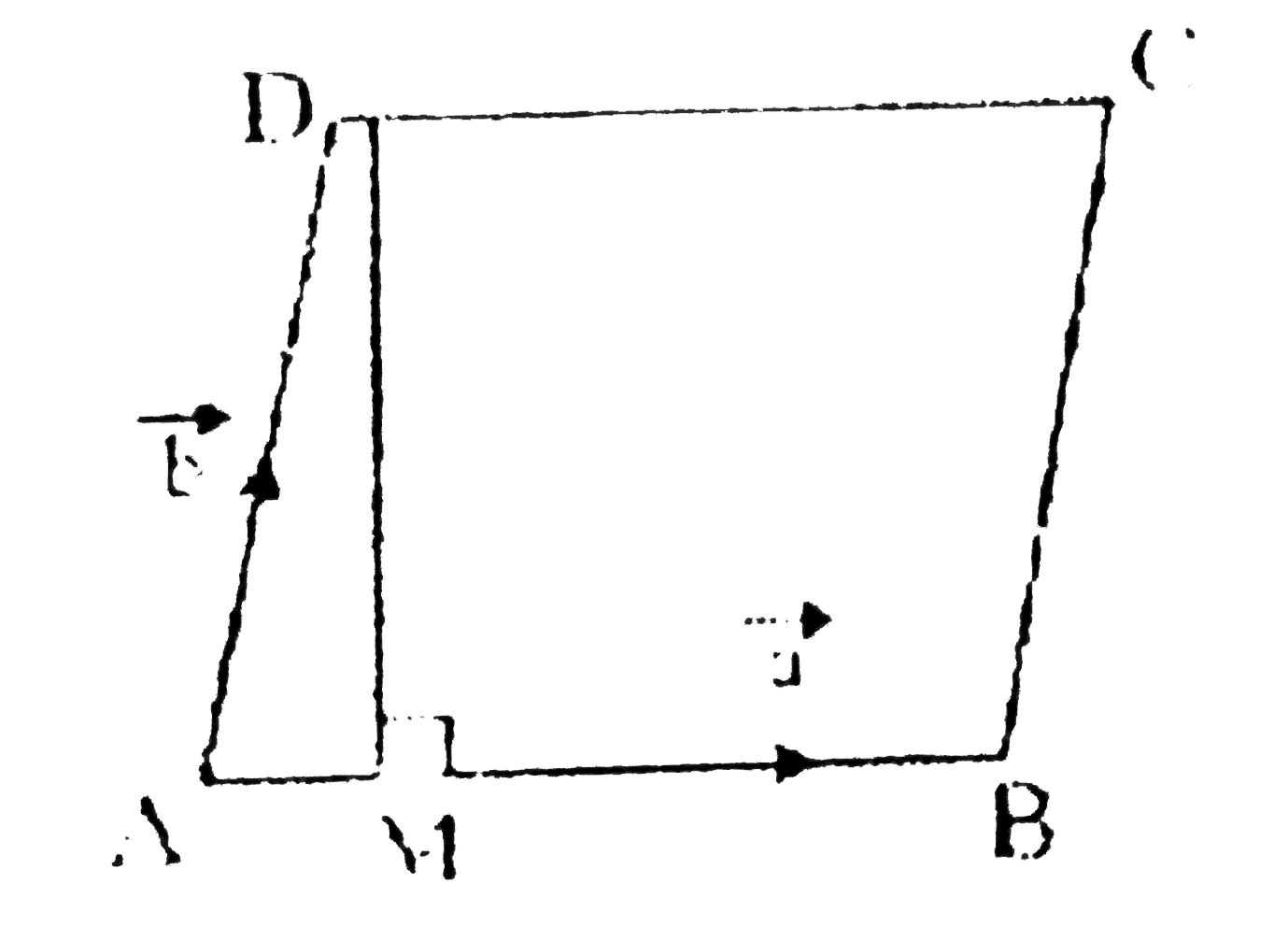
We have
AM= projection of becb on →a=→a.→b|→a|
−−→AM=(→a.→b|→a|2)→a
Now in
−−→AD=−−→AM+−−→MD or −−→DM=−−→AM−−−→AD
⇒−−→DM=(→a.→b)→a|→a|2−→b
1|→a|2[(→a.→b)→a−|→a|2→b]
⇒−−→MD=1|→a|2[|→a|2→b−(→a.→b)→a]
Now →a×(→a×→b)|→a|2=1|→a|2[(→a.→b)→a−(→a.→a)b→b]
−−→DM
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART : 1MATHEMATICS SEC - 1
1 Video
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART : 1MATHEMATICS
9 Videos
- TEST PAPERBOOK - RESONANCECHAPTER - TEST PAPEREXERCISE - CHEMISTRY
37 Videos
- TEST SERIESBOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - MATHEMATICS
131 Videos
Similar Questions
If vectors →aand→b are two adjacent sides of parallelograsm then the vector representing the altitude of the parallelogram which is perpendicular to →a is (A) →b+→b×→a|→a|2 (B) →a.→b→b∣∣2 (C) →b−→b.→a(|→a|)2) (D) →a×(→b×→a)→b∣∣20
View SolutionA Parallelogram is constructed with a and b as adjacent sides such that |-|=a and | b-b The vector which coincides with the altitude of the parallelogram and is perpendicular to the vector a is.
View Solution
Knowledge Check
If →a and →b are two unit vectors, then the vector (→a+→b)×(→a×→b) is parallel to the vector
A→a+→bB→a−→bC2→a+→bD2→a−→bWhich of the following is the unit vector perpendicular to →A and →B
AˆA׈BAbsinθeBˆA׈BAbcosθC→A×→BAbsinθD→A×→BAbcosθIf →aand→b are othogonal unit vectors, then for a vector →r non - coplanar with →aand→b vector →r×→a is equal to
A[→r→a→b]→b−(→r.→b)(→b×→a)B[→r→a→b](→a+→b)C[→r→a→b]→a+(→r.→a)→a×→bDnone of these
There are two vectors →A=3ˆi+ˆjand→B=ˆj+2ˆk. For these two vectors -
(a) If →A&→B are the adjacent sides of a parallelogram then find the magnitude of its area.
(b) Find a unit vector which is perpendicular to both →A&→B.
View SolutionThere are two vectors →A=3ˆi+ˆj and →B=ˆj+2ˆk. For these two vectors-
(a) Find the component of →A along →B in vector form.
(b) If →A&→B are the adjacent sides of a parallalogram then find the magnitude of its area.
(c) Find a unit vector which is perpendicular to both →A&→B.
View SolutionIf →aand→b are the vectors determined by two adjacent sides of a regular hexagon ABCDEF, find the vector determined by the ther sides taken in order. Also find −−→ADand−−→CE in terms of →aand→b.
View SolutionIf ∣∣→a+→b∣∣=∣∣→a−→b∣∣ then the vectors →a and →b are adjacent sides of
View SolutionIf →A and →B are two vectors, then which of the following is wrong?
View Solution