A plane mirror rotating at an angular velocity of 3 radian/s reflects a light beam. The angular velocity of the reflected beam is -
3rad/s
6rad/s
9rad/s
12rad/s
The correct Answer is:B
To find the angular velocity of the reflected beam when a plane mirror rotates, we can follow these steps:
1. Understand the relationship between the mirror's rotation and the reflected beam:
- When a plane mirror rotates by an angle θ, the angle of the reflected beam changes by an angle of 2θ. This is due to the law of reflection, which states that the angle of incidence is equal to the angle of reflection.
2. Define the angular velocity of the mirror:
- Given that the angular velocity of the mirror (ω_m) is 3 radian/s, we can express this as:
ωm=dθdt=3 rad/s
3. Relate the angular velocity of the reflected beam to that of the mirror:
- Since the reflected beam rotates by an angle of 2θ when the mirror rotates by θ, the angular velocity of the reflected beam (ω_r) can be expressed as:
ωr=d(2θ)dt=2dθdt=2ωm
4. Substitute the value of the mirror's angular velocity:
- Now, substituting the value of ω_m into the equation for ω_r:
ωr=2×3 rad/s=6 rad/s
5. Determine the direction of the angular velocity:
- The reflected beam's angular velocity is in the opposite direction to the mirror's rotation. Therefore, we express this as:
ωr=−6 rad/s
Final Answer:
The angular velocity of the reflected beam is -6 rad/s.
---
- When a plane mirror rotates by an angle θ, the angle of the reflected beam changes by an angle of 2θ. This is due to the law of reflection, which states that the angle of incidence is equal to the angle of reflection.
- Given that the angular velocity of the mirror (ω_m) is 3 radian/s, we can express this as:
ωm=dθdt=3 rad/s
- Since the reflected beam rotates by an angle of 2θ when the mirror rotates by θ, the angular velocity of the reflected beam (ω_r) can be expressed as:
ωr=d(2θ)dt=2dθdt=2ωm
- Now, substituting the value of ω_m into the equation for ω_r:
ωr=2×3 rad/s=6 rad/s
- The reflected beam's angular velocity is in the opposite direction to the mirror's rotation. Therefore, we express this as:
ωr=−6 rad/s
The angular velocity of the reflected beam is -6 rad/s.
Topper's Solved these Questions
Similar Questions
A wheel is rotating with an angular velocity of 3rads−1. If the angular acceleration is 2rads−1 then calculate its angular velocity after 5 second.
View SolutionA rod is rotating with an angular velocity of 3πt3rad / s. The angle rotated by the rod from t=0 to the time when it has an angular velocity of 24π rad/sec is given by απ radian. Find α2.
View Solution
Knowledge Check
A fly wheel is rotating about its own axis at an angular velocity 11rads−1, its angular velocity in revolation per minute is
A105B210C315D420A particle is in circular motion in a horizotantal plane. It has angular velocity of 10πrad/s at the end of 2 s and angular velocity 15 πrad/s at the end of 4s. The angular acceleration of particle is
A5πrad/s2B2.5πrad/s2C6πrad/s2D16πrad/s2A particle attached to a string is rotating with a constant angular velocity and its angular momentum is L. If the string is halved and angular velocity is kept constant, the angular momentum will be
AL/4BL/2CLD2L
A wheel starting from rest via rotating with a constant angular velocity of 3 rad s−1. What is its angular acceleration after 4 s?
View SolutionSpotlight S rotates in a horizontal plane with constant angular velocity of 0.1 radian //second.Thespotoflightpmovesalongthewallatadistanceof3 m .Thevelocityofthespotpwhentheta = 45(@)(see−fig.)is……….. m//s
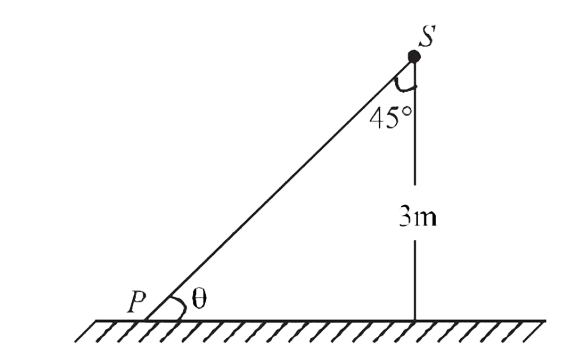
View SolutionA particle rotates in a circle with angular speed ω0. A retarding force decelerates it such that angular deceleration is always proportional to square root of angular velocity. Find the mean angular velocity of the particle averaged over the whole time of rotation.
View SolutionWhat is the angular velocity of a geostationary satellite in radian per hour ?
View SolutionIf ωE is the angular velocity of the earth rotating about its own axis and ωH is the angular velocity of the hour of a clock , then
View Solution
