A ball suspended by a thread swings in a vertical plane so that its acceleration in the extreme position and lowest position are equal. The angle of thread deflection in the extreme position will be - 2
tan−1(2)
tan−1(√2)
tan−1(12)
2tan−1(12)
The correct Answer is:D
To solve the problem, we need to analyze the forces acting on the ball in both the extreme position and the lowest position of the swing.
Step 1: Analyze the forces in the lowest position
When the ball is at the lowest position, the forces acting on it are:
- The tension T in the thread acting upwards.
- The weight mg acting downwards.
At this position, the ball is in circular motion, so the net centripetal force is provided by the difference between the tension and the weight:
T−mg=mv2L
where L is the length of the thread and v is the speed of the ball at the lowest position.
Step 2: Analyze the forces in the extreme position
In the extreme position (where the thread makes an angle θ with the vertical), the forces acting on the ball are:
- The tension T in the thread acting along the thread.
- The weight mg acting vertically downwards.
The components of the forces can be resolved:
- The vertical component of tension must balance the weight:
Tcos(θ)=mg
- The horizontal component provides the centripetal force:
Tsin(θ)=mv2L
Step 3: Set the accelerations equal
According to the problem, the acceleration in the extreme position and the lowest position are equal. The acceleration at the lowest position can be expressed as:
alowest=v2L
At the extreme position, the radial acceleration can be expressed as:
aextreme=gsin(θ)
Setting these equal gives us:
v2L=gsin(θ)
Step 4: Substitute for T
From the equation Tcos(θ)=mg, we can express T as:
T=mgcos(θ)
Substituting T into the horizontal force equation:
mgcos(θ)sin(θ)=mv2L
This simplifies to:
mgtan(θ)=mv2L
Step 5: Combine the equations
Now we have two equations:
1. v2L=gsin(θ)
2. gtan(θ)=v2L
Setting these equal gives:
gsin(θ)=gtan(θ)
This implies:
sin(θ)=tan(θ)cos(θ)
Using the identity tan(θ)=sin(θ)cos(θ), we can simplify to:
sin(θ)=sin(θ)
This is always true, but we need to find the angle θ.
Step 6: Solve for θ
From the relationship tan(θ)=1, we find:
θ=45∘
Final Answer
The angle θ of thread deflection in the extreme position will be 45∘.
When the ball is at the lowest position, the forces acting on it are:
- The tension T in the thread acting upwards.
- The weight mg acting downwards.
T−mg=mv2L
where L is the length of the thread and v is the speed of the ball at the lowest position.
In the extreme position (where the thread makes an angle θ with the vertical), the forces acting on the ball are:
- The tension T in the thread acting along the thread.
- The weight mg acting vertically downwards.
- The vertical component of tension must balance the weight:
Tcos(θ)=mg
- The horizontal component provides the centripetal force:
Tsin(θ)=mv2L
According to the problem, the acceleration in the extreme position and the lowest position are equal. The acceleration at the lowest position can be expressed as:
alowest=v2L
At the extreme position, the radial acceleration can be expressed as:
aextreme=gsin(θ)
Setting these equal gives us:
v2L=gsin(θ)
From the equation Tcos(θ)=mg, we can express T as:
T=mgcos(θ)
Substituting T into the horizontal force equation:
mgcos(θ)sin(θ)=mv2L
This simplifies to:
mgtan(θ)=mv2L
Now we have two equations:
1. v2L=gsin(θ)
2. gtan(θ)=v2L
gsin(θ)=gtan(θ)
This implies:
sin(θ)=tan(θ)cos(θ)
Using the identity tan(θ)=sin(θ)cos(θ), we can simplify to:
sin(θ)=sin(θ)
This is always true, but we need to find the angle θ.
From the relationship tan(θ)=1, we find:
θ=45∘
The angle θ of thread deflection in the extreme position will be 45∘.
Topper's Solved these Questions
Similar Questions
(a) A ball, suspended by a thread, swings in a vertical plane so that the magnitudes of its acceleration in the extreme and the lowest positions are equal. Find the maximum deflection of the thread with respect to the vertical.
( b) The kinetic energy of a particle moving in a circle of radius R depens on the distance covered as T=as2 , where 'a' is a constant. Find the magnitude of the force acting on the particle as a function of s.
View SolutionA small bob suspended by a thread swings in a vertical plane so that angle made by thread in extreme positions with the vertical is θ=sin−1(45) What is the ratio of acceleration of bob in extreme position to its acceleration in lowest position?
View Solution
Knowledge Check
A ball suspended by a thread swings in a vertical plane so that its acceleration in the extreme position and lowest position are equal. The angle of thread deflection in the extreme position will be - 2
Atan−1(2)Btan−1(√2)Ctan−1(12)D2tan−1(12)A ball attached to one end of a stringj swings in a vertical plane such that its acceleration at point A (exterme posiuion) is eqal to its acceleration at point B (mean posirion), The angle θ is
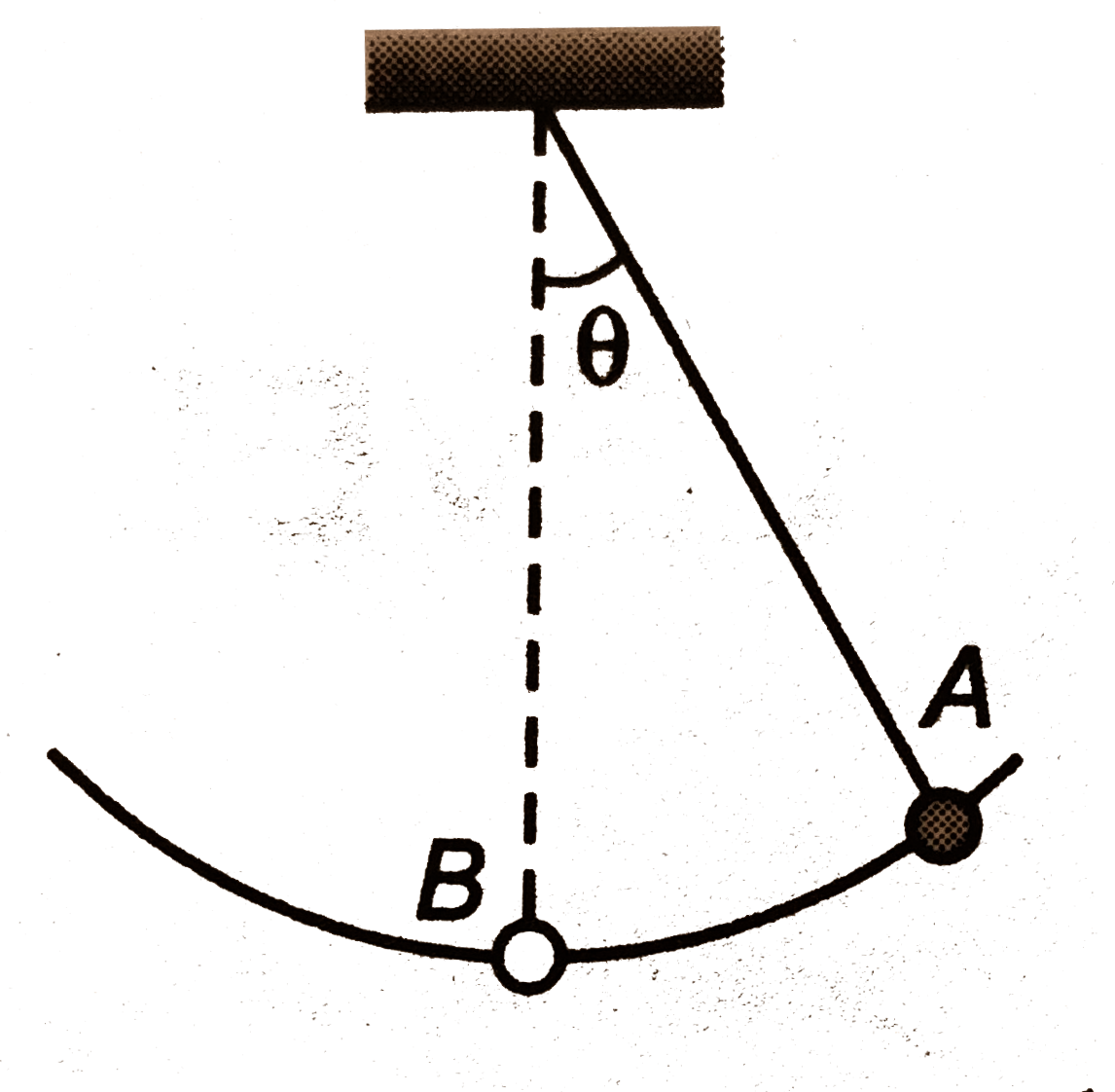 Acos−1(25)Bcos−1(45)Ccos−1(35)DNone of these
Acos−1(25)Bcos−1(45)Ccos−1(35)DNone of theseParticle moves from extreme position to mean position, its
Akinetic energy increases, potential energy decreasesBkinetic energy decreases, potential increasesCboth remains constantDpotential energy becomes zero and kinetic energy remains contant
A rod of mass m and length l suspended from a point swings in a vertica plane such that magnitude of acceleration of its C.M. at extreme points is same as that at the mean point then :
View SolutionStudy the diagram given below and answer the following question.

Name the extreme position of the swing.
View SolutionThe velocity at mean position and acceleration at the extreme position have the phase difference of
View SolutionA short boy sits on a seat suspended by a light string from a fixed point O and starts swinging in a vertical plane from the extreme position P with a small amplitude the graph which shows the variation of the tension in the string with time 't' is:

View SolutionThe acceleration of a particle performing S.H.M. at extreme position is
View Solution

