A cylinder piston of mass M sides smoothlly inside a long cylinder closed at and enclesing a cartin mass of gas The cylinder is kept with its axis horizantal if the pistan is distanced from its equations positions it oscillation simple harmoniically .THe period of oscillation will be

T=2πS√(MhPA)
T=2π√(MAPh)
T=2π√(MPAh)
T=2π√MPhA
Step by step video & image solution for A cylinder piston of mass M sides smoothlly inside a long cylinder closed at and enclesing a cartin mass of gas The cylinder is kept with its axis horizantal if the pistan is distanced from its equations positions it oscillation simple harmoniically .THe period of oscillation will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionA particle of mass 4kg moves simple harmonically such that its PE (U) varies with position x, as shown. The period of oscillations is :-
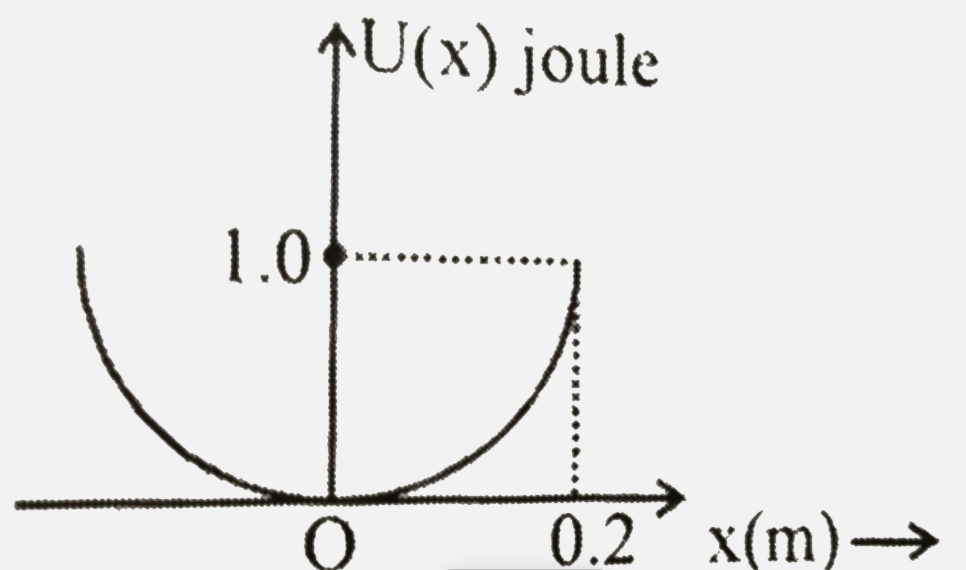
View Solution
Knowledge Check
A cylinder piston of mass M sides smoothly inside a long cylinder closed at and enclosing a certain mass of gas The cylinder is kept with its axis horizontal if the piston is distanced from its equations positions it oscillation simple harmonically .The period of oscillation will be
 AT=2π√(MhPA)BT=2π√(MAPb)CT=2π√(MPAh)DT=2π√MPhA
AT=2π√(MhPA)BT=2π√(MAPb)CT=2π√(MPAh)DT=2π√MPhAA cylindrical piston of mass M slides smoothly inside a long cylinder closed at one end, enclosing a certain mass of gas. The cylinder is kept with its axis horizontal. If the piston is disturbed from its equilibrium position, it oscillates simple harmonically. Pressure inside the gas in equilibrium is P. Consider the piston to be diathermic so that process is isothermal the period of oscillation will be:
 AT=2π√(MhPA)BT=2π√(MAPh)CT=2π√(MPAh)DT=2π√MPhA
AT=2π√(MhPA)BT=2π√(MAPh)CT=2π√(MPAh)DT=2π√MPhAThe moment of inertia of cylinder of radius a, mass M and height h about an axis parallel to the axis of the cylinder and distance b from its centre is :
A12M(a2+2b2)B12M(2a2+b2)C12M(a2+b2)D12M(a23+b212)
A small point mass m has a charge q, which is constrained to move inside a narrow frictionless cylinder, At the bae of the cylinder is point mass of charge Q having the same sign as q. If the mass m is displaced by a small amount from its equilibrium position and released. it will exhibit simple harmonic motion. Find the angular frequency of the mass?

View Solution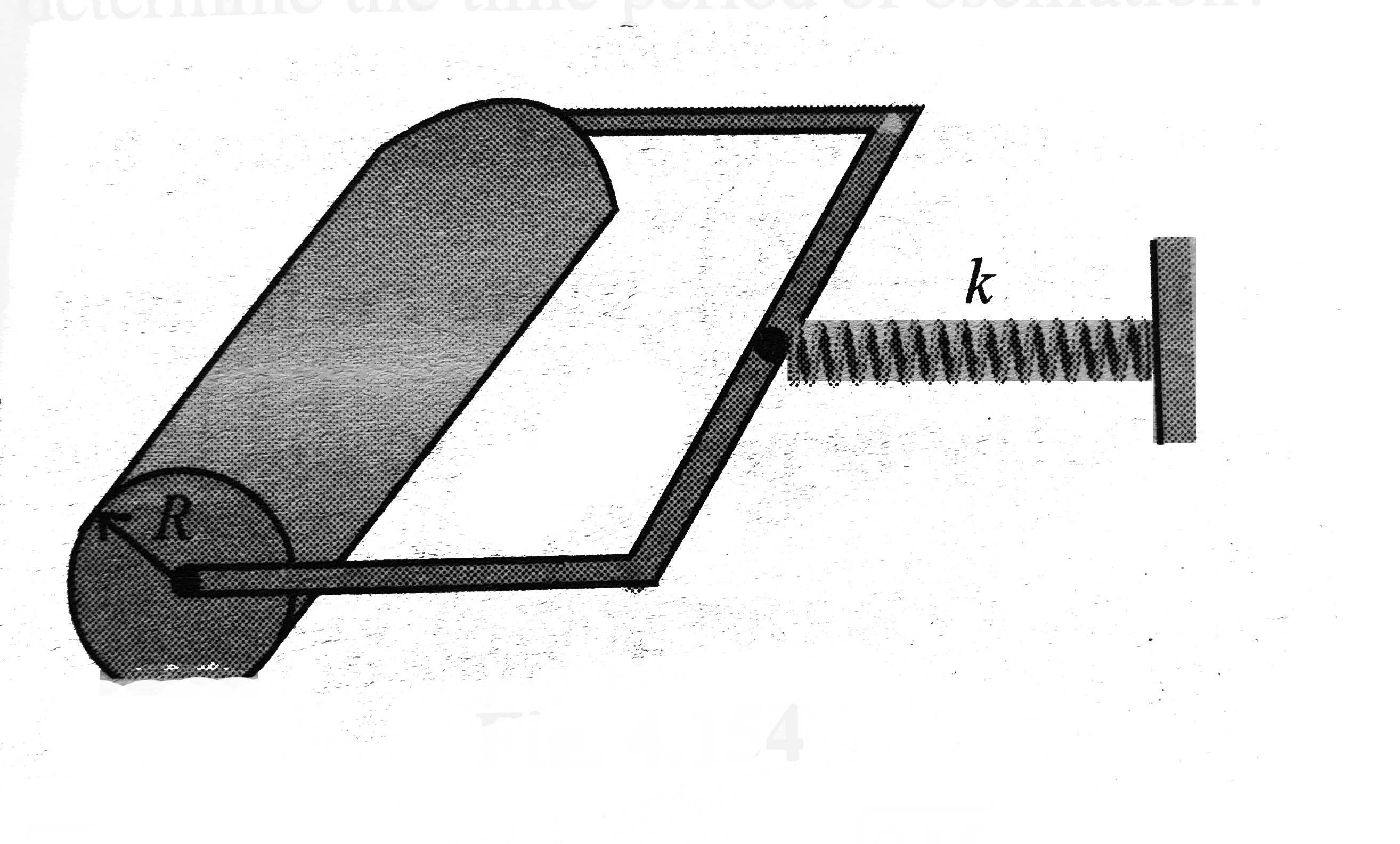
A soil cylinder of mass M and radius R is connected to a spring as shown in fig. The cylinder is placed on a rough horizontal surface. All the parts except the cylinder shown in the figure are light. If the cylinder is displaced slightly from its mean position and released, so that it performs pure rolling back and forth about its equilibrium position, determine the time period of oscillation?
View SolutionAn cylinder of mass m is rotated about its axis by an angular velocity ω and lowered gently on an inclined plane as shown in figure. Then :
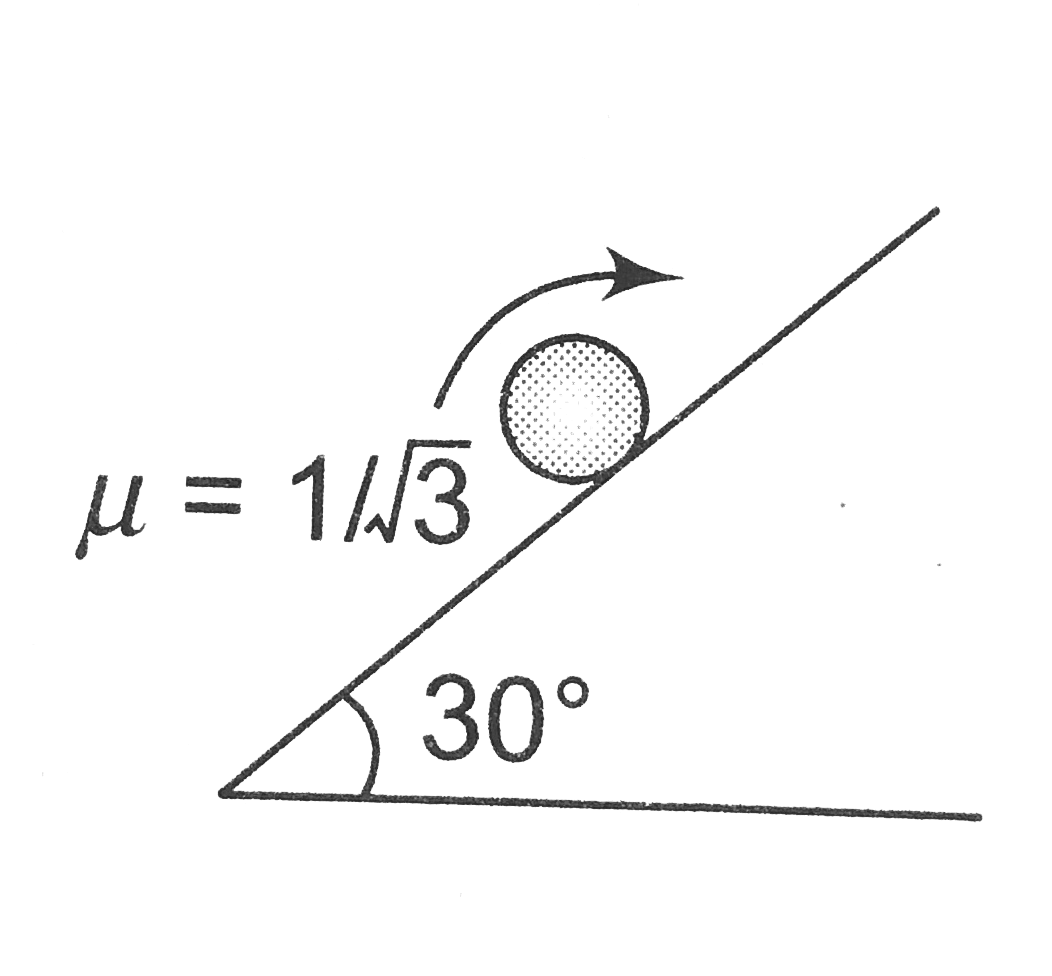 .
.
View SolutionMoment of inertia of a hollow cylinder of mass M and radius r about its own axis is
View SolutionA particle of mass 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is

View Solution

