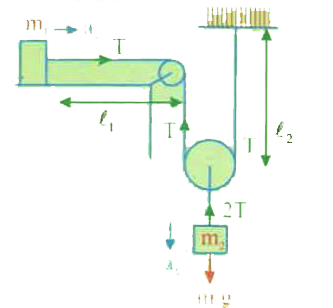
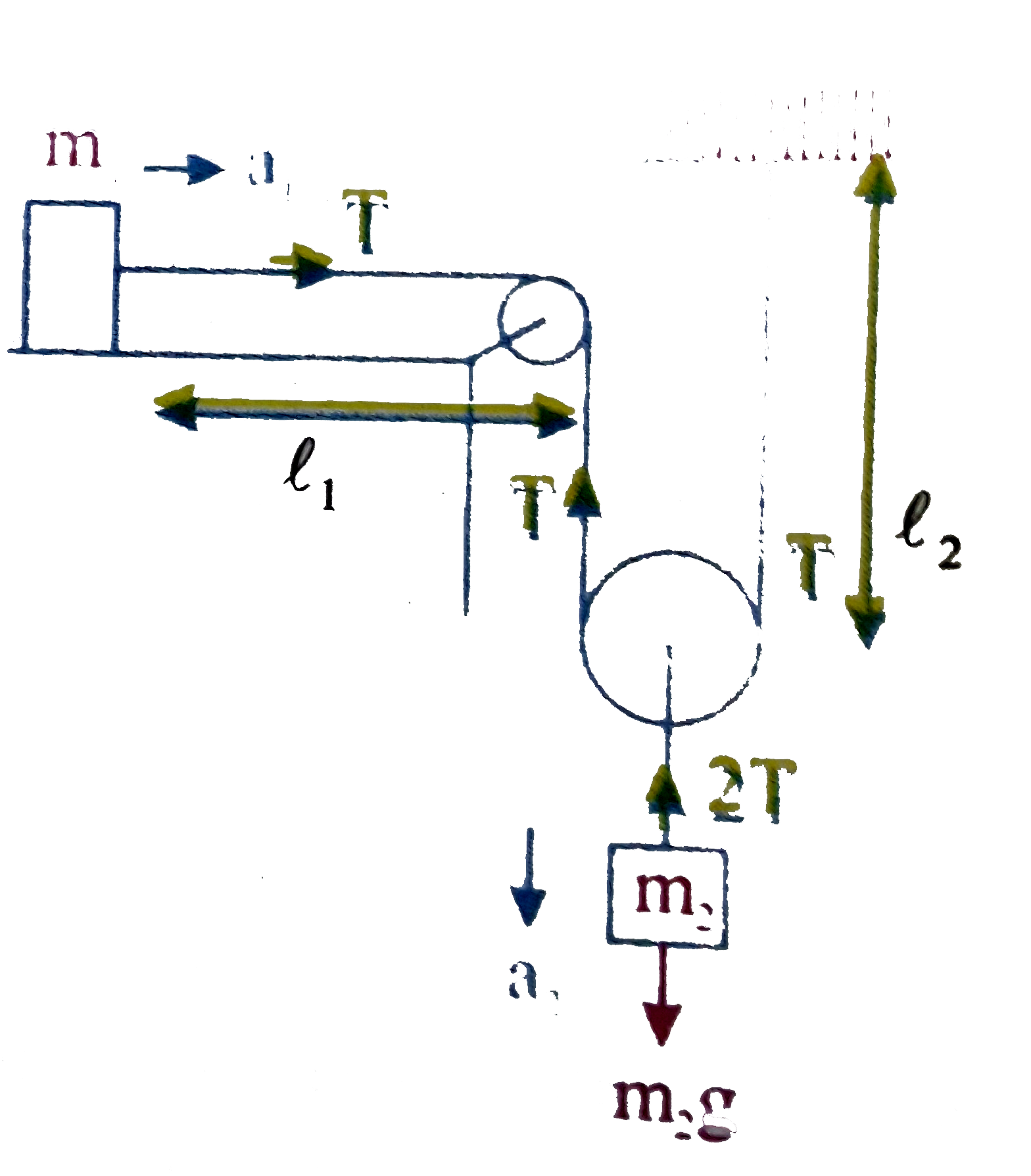
Statement– 1 : In the given fig. $a = (\frac{m_{2} - m_{1}}{m_{1} + m_{2}}) g$
Statement– 2 : In the given fig., $T = \frac{m_{1} + m_{2}}{2 m_{1} m_{2}}$

Statement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1.

Statement-1 is True, Statement-2 is True, Statement-2 is NOT a correct explanation for Statement-1.

Statement -1 is False, Statement-2 is True

Statement -1 is True, Statement-2 is False

Video Solution

Answer

Step by step video & image solution for Statement– 1 : In the given fig. "a"=(("m"_(2)-"m"_(1))/("m"_(1)+"m"_(2)))"g" Statement– 2 : In the given fig., "T"=("m"_(1)+"m"_(2))/(2"m"_(1)"m"_(2)) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS LAWS OF MOTION

Topper's Solved these Questions

Knowledge Check

Consider the case of two bodies of masses $m_{1} and m_{2}$ which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations:

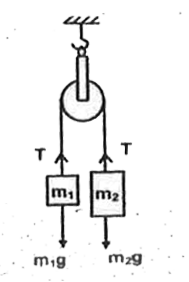
(i) when $m_{1} > m_{2}$ . In this case
$a = (\frac{m_{1} - m_{2}}{m_{1} + m_{2}}) g and T = (\frac{2 m_{1} m_{2}}{m_{1} + m_{2}}) g$
(ii) when $m_{2} > m_{1}$ . In this case
$a = (\frac{m_{2} - m_{1}}{m_{1} + m_{2}}) g and T = (\frac{2 m_{1} m_{2}}{m_{1} + m_{2}}) g$
(iii) When $m_{1} = m_{2} = m$ . In this case $a = 0, T = m g$
What is the tension in the string?
A60N
B75N
C100N
D600N
Consider the case of two bodies of masses $m_{1} and m_{2}$ which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations:

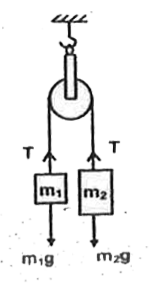
(i) when $m_{1} > m_{2}$ . In this case
$a = (\frac{m_{1} - m_{2}}{m_{1} + m_{2}}) g and T = (\frac{2 m_{1} m_{2}}{m_{1} + m_{2}}) g$
(ii) when $m_{2} > m_{1}$ . In this case
$a = (\frac{m_{2} - m_{1}}{m_{1} + m_{2}}) g and T = (\frac{2 m_{1} m_{2}}{m_{1} + m_{2}}) g$
(iii) When $m_{1} = m_{2} = m$ . In this case $a = 0, T = m g$
If the pulley is pulled upward with acceleration equal to the acceleration due to gravity, what will be the tension in the string?
A75N
B150N
C300N
D500N
Consider the case of two bodies of masses $m_{1} and m_{2}$ which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations:

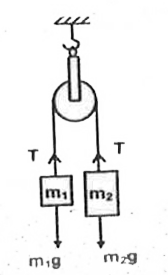
(i) when $m_{1} > m_{2}$ . In this case
$a = (\frac{m_{1} - m_{2}}{m_{1} + m_{2}}) g and T = (\frac{2 m_{1} m_{2}}{m_{1} + m_{2}}) g$
(ii) when $m_{2} > m_{1}$ . In this case
$a = (\frac{m_{2} - m_{1}}{m_{1} + m_{2}}) g and T = (\frac{2 m_{1} m_{2}}{m_{1} + m_{2}}) g$
(iii) When $m_{1} = m_{2} = m$ . In this case $a = 0, T = m g$
If $m_{1} = 10 k g, m_{2} = 6 k g and g = 10 m / s^{2}$ then what is the acceleration of masses?
A $2.5 m / s^{2}$
B $5 m / s^{2}$
C $20 m / s^{2}$
D $40 m / s^{2}$