In triangle XYZ (not shown), the measure of ∠Y is 90∘,YZ=12,andXZ=15. Triangle HJK is similar to triangle XYZ, where vertices H, J, and K corresponds ot vertices X, Y, and Z, respectively, and each side of triangle HJK is 15 the length of the corresponding side of triangle XYZ. What is the value of tanK?
The correct Answer is:C, D
To solve the problem step by step, we will follow these instructions:
Step 1: Identify the given information in triangle XYZ
- Angle Y = 90°
- YZ = 12 units (this is the base)
- XZ = 15 units (this is the hypotenuse)
Step 2: Use the Pythagorean theorem to find XY
The Pythagorean theorem states that in a right triangle, the square of the hypotenuse (XZ) is equal to the sum of the squares of the other two sides (XY and YZ).
XZ2=XY2+YZ2
Substituting the known values:
152=XY2+122
Calculating the squares:
225=XY2+144
Now, isolate XY^2:
XY2=225−144
XY2=81
Taking the square root to find XY:
XY=√81=9 units
Step 3: Identify the similar triangle HJK
Since triangle HJK is similar to triangle XYZ and each side of triangle HJK is 15 the length of the corresponding side of triangle XYZ, we can find the lengths of the sides of triangle HJK.
- HJ (corresponding to XY) = 15×9=95 units
- JK (corresponding to YZ) = 15×12=125 units
- HK (corresponding to XZ) = 15×15=3 units
Step 4: Find tan K
In triangle HJK, we need to find tanK. Since triangle HJK is similar to triangle XYZ, the angles are corresponding.
Using the definition of tangent:
tanK=oppositeadjacent=HJJK
Substituting the values we found:
tanK=95125=912=34
Conclusion
The value of tanK is 34.
---
- Angle Y = 90°
- YZ = 12 units (this is the base)
- XZ = 15 units (this is the hypotenuse)
The Pythagorean theorem states that in a right triangle, the square of the hypotenuse (XZ) is equal to the sum of the squares of the other two sides (XY and YZ).
XY2=81
Since triangle HJK is similar to triangle XYZ and each side of triangle HJK is 15 the length of the corresponding side of triangle XYZ, we can find the lengths of the sides of triangle HJK.
- JK (corresponding to YZ) = 15×12=125 units
- HK (corresponding to XZ) = 15×15=3 units
In triangle HJK, we need to find tanK. Since triangle HJK is similar to triangle XYZ, the angles are corresponding.
The value of tanK is 34.
Topper's Solved these Questions
Similar Questions
In triangle ABC, the measure of ∠B is 90∘, BC = 16, and AC = 20. Triangle DEF is similar to triangle ABC, where vertices D, E, and F correspond to vertices A, B, and C, respectively, and each side of triangle DEF is 13 the length of the corresponding side of triangle ABC. What is the value of sin F ?
View SolutionThe perimeters of two similar triangles are 25cm and 15cm respectively. If one side of first triangle is 9cm, what is the corresponding side of the other triangle?
View Solution
Knowledge Check
In triangle PQR. ∠Q is a right angle, QR=24, and PR=26. Triangle YXZ is similar to triangle PQR, where vertices X, Y, and Z correspond to vertices P, Q, and R, respectively, and each side of triangle XYZ is 12 the length of the corresponding side of triangle PQR. What is the value of sin Z?
A513B512C1213D125Triangle PQR is a right tyriangle with the 90∘ angle at vertex Q. The length of side PQ is 25 and the length of side QR is 60. Triangle STU is similar to trianlge PRQ. The vertices S,T,and U correspond to vertices P, Q, and R, respectively. Each side of triangle STU is 110 the length of the corresponding side of triangle PRQ. What is the value of cos∠U ?
A513B512C56D1213In the triangle below , the lengths of the two given sides are measured in centimeters. What is the value , in centimeters, of x ?
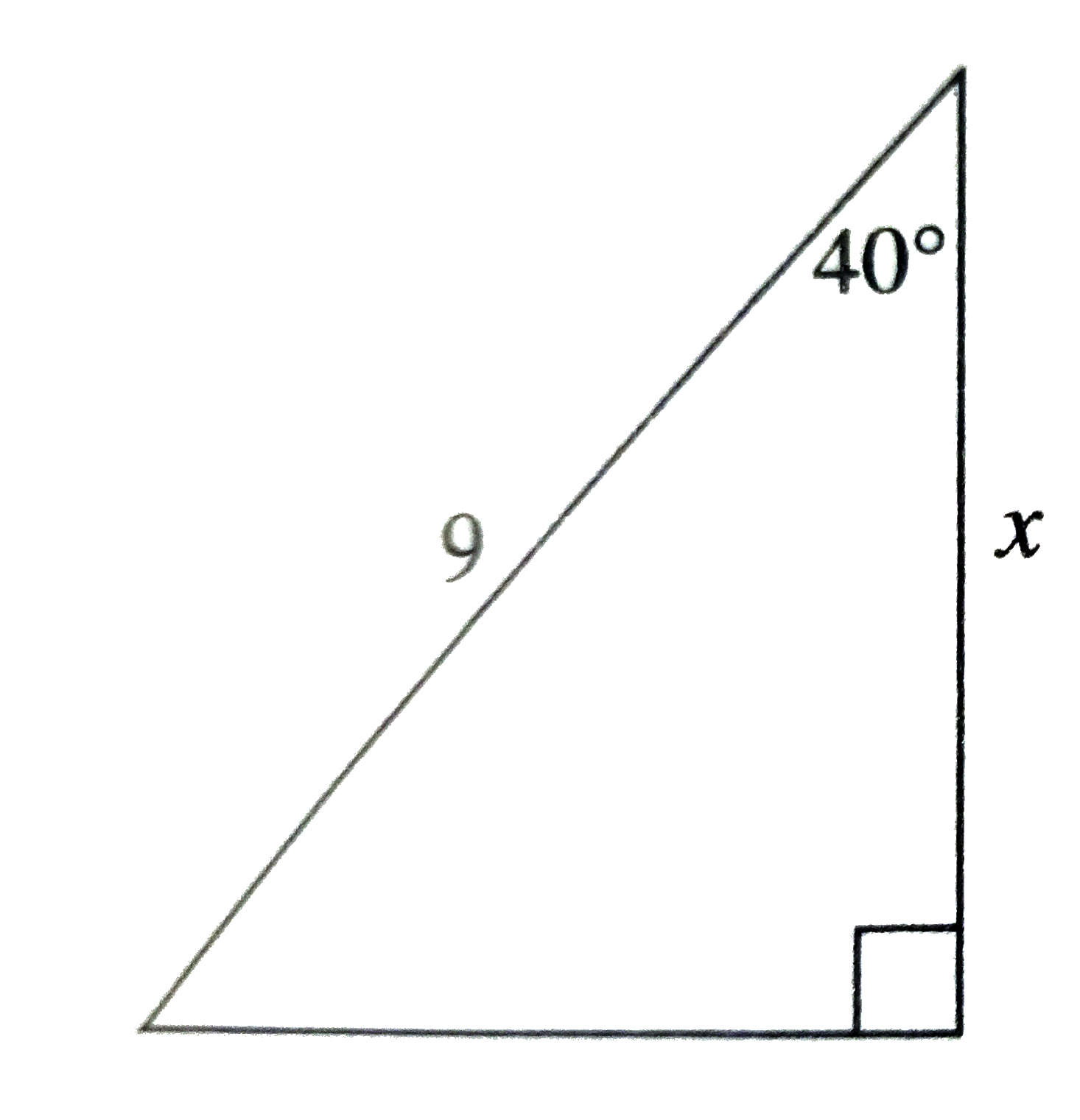 A9sin40∘B9sin50∘C9cos50∘D9tan40∘
A9sin40∘B9sin50∘C9cos50∘D9tan40∘
The perimeters of two similar triangles are 30cm and 20cm respectively. If one side of the first triangle is 12cm, determine the corresponding side of the second triangle.
View SolutionConstruct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it where sides are 23of the corresponding sides of the first triangle.
View SolutionFind the area of triangle whose sides are 9 cm, 12cm and 15 cm. Also, find the length of altitude corresponding to the largest side of the triangle.
View SolutionConstruct a triangle similar to a given triangle ABC such that each of its sides is 23rd of the corresponding sides of the triangle ABC. It is given that AB=4cm, BC=5cm and AC=6cm .
View SolutionTwo similar triangles have perimeters in the ratio 3:5. The sides of the smaller triangle measure 3 cm, 5 cm, and 7 cmd, respectively. What is the perimeter, in centimeters, of the larger triangle?
View Solution

