A cylinder has a volume of 72π cubic inches and a height of 8 inches. If the height is increased by 4 inches, what will be the new volume of the cylinder in cubic inches?
76π
108π
328π
576π
The correct Answer is:B
To find the new volume of the cylinder after increasing its height, we can follow these steps:
Step 1: Understand the given information
We are given:
- Original volume of the cylinder, V=72π cubic inches
- Original height of the cylinder, h=8 inches
Step 2: Calculate the radius of the original cylinder
The volume V of a cylinder is given by the formula:
V=πr2h
Where r is the radius and h is the height. We can rearrange this formula to find the radius:
r2=Vπh
Substituting the known values:
r2=72ππ⋅8=728=9
Taking the square root:
r=3 inches
Step 3: Calculate the new height of the cylinder
The height is increased by 4 inches:
New height=8+4=12 inches
Step 4: Calculate the new volume of the cylinder
Now we can use the volume formula again with the new height:
Vnew=πr2hnew
Substituting the radius and the new height:
Vnew=π(32)(12)=π(9)(12)=108π cubic inches
Final Answer
The new volume of the cylinder is 108π cubic inches.
---
We are given:
- Original volume of the cylinder, V=72π cubic inches
- Original height of the cylinder, h=8 inches
The volume V of a cylinder is given by the formula:
V=πr2h
Where r is the radius and h is the height. We can rearrange this formula to find the radius:
r2=Vπh
Substituting the known values:
r2=72ππ⋅8=728=9
Taking the square root:
r=3 inches
The height is increased by 4 inches:
New height=8+4=12 inches
Now we can use the volume formula again with the new height:
Vnew=πr2hnew
Substituting the radius and the new height:
Vnew=π(32)(12)=π(9)(12)=108π cubic inches
The new volume of the cylinder is 108π cubic inches.
Topper's Solved these Questions
Similar Questions
A laboratory supply company produces graduated cylinders, each with an internal radius of 2 inches and an internal height between 7.75 inches and 8 inches. What is one possible volume, rounded to the nearest cubic inch, of a graduated cylinder produced by this company?
View SolutionA sealed cylindrical can holds three tennis balls each with diameter of 2.5 inches. If the can is designed to have the smallest possible volume, find the number of cubic inches of unoccopied space inside the can correct to the nearest tenth of a cubic inch.
View Solution
Knowledge Check
If the height and radii of the cylinder halved then the volume of the cylinder becomes ____
A8 times the original volumeB4 times the original volumeC18 time the original volumeDit will rename sameA right circular cone has a volume of 24π cubic inches. If the height of the cone is 2 inches, what is the radius, in inches, of the base of the cone?
A2√3B6C12D36
In the figure above, the radius of the base of the cylinder is half its height. What is the approximate volume of the cylinder in cubic inches?A28B57C117D170
The height h of a cylinder equals the circumference of the cylinder. In terms of h, what is the volume of the cylinder?
View SolutionFind the volume of a cone with a slant heitght of 15 inches and a base with a 16- inch diameter.
View SolutionIf a sector of a circle has an arc length of 2π inches and an area of 6π square inches, what is the length of the radius of the circle?
View Solution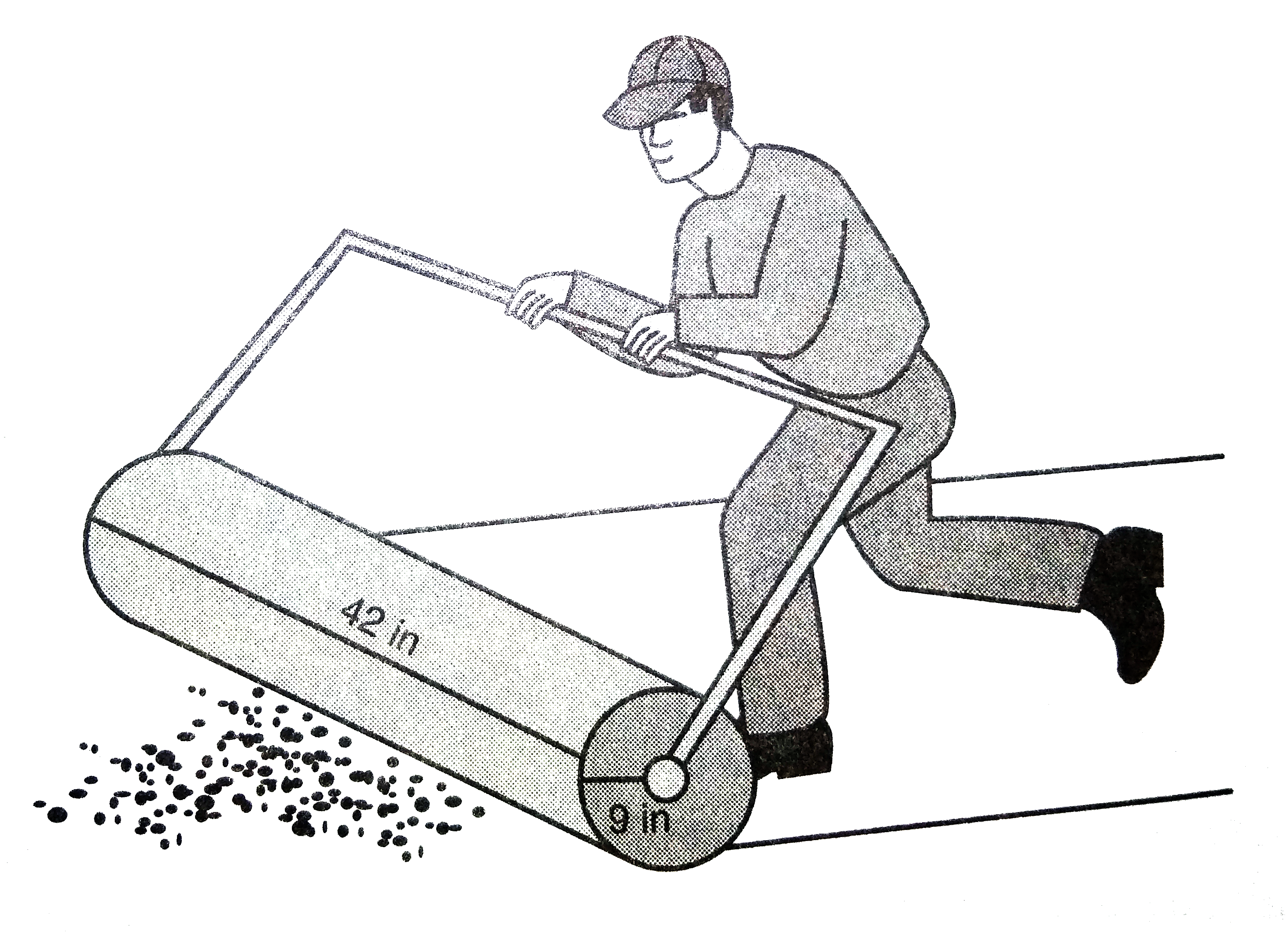
As shown in the figure above, a worker uses a cylindrical roller to help pave a road. The roller has a radius of 9 inches and a width of 42 inches. To the nearest square inch, what is the area of the roller covers in one complete rotation?
View SolutionThe volume of a rectangle box is 144 cubic inches. The height of the solid is 8 inches. Which measurements, in inches, could be the dimensions of the base?
View Solution
