If f(x) is a linear function and the slope of y=f(x) is 12, what is the slope of y=f−1(x) ?
−2
−12
12
2
The correct Answer is:D
To find the slope of the inverse function y=f−1(x) given that the slope of y=f(x) is 12, we can use the relationship between the slopes of a function and its inverse.
1. Understand the relationship between the slopes:
The slope of the function f(x) is denoted as m. For the inverse function f−1(x), the slope m′ is given by the formula:
m′=1m
where m is the slope of f(x).
2. Identify the given slope:
From the problem, we know that the slope of f(x) is:
m=12
3. Calculate the slope of the inverse function:
Using the formula for the slope of the inverse function:
m′=1m=112=2
4. Conclusion:
Therefore, the slope of y=f−1(x) is:
m′=2
Final Answer:
The slope of y=f−1(x) is 2.
The slope of the function f(x) is denoted as m. For the inverse function f−1(x), the slope m′ is given by the formula:
m′=1m
where m is the slope of f(x).
From the problem, we know that the slope of f(x) is:
m=12
Using the formula for the slope of the inverse function:
m′=1m=112=2
Therefore, the slope of y=f−1(x) is:
m′=2
The slope of y=f−1(x) is 2.
Topper's Solved these Questions
- FUNCTIONS Book:KAPLANChapter:FUNCTIONS Exercise:FUNCTIONS FOLLOW - UP TEST
Explore 6 Videos
- EXPONENTS, RADICALS, POLYNOMIALS, AND RATIONAL EXPRESSIONS Book:KAPLANChapter:EXPONENTS, RADICALS, POLYNOMIALS, AND RATIONAL EXPRESSIONS Exercise:Multiple Choice Question
Explore 20 Videos
- FUNCTIONS AND FUNCTION NOTATIONBook:KAPLANChapter:FUNCTIONS AND FUNCTION NOTATIONExercise:Multiple Choice Question
Explore 20 Videos
Similar Questions
Let f:[0,2π]→[−3,3] be a given function defined at f(x)=3cosx2. The slope of the tangent to the curve y=f−1(x) at the point where the curve crosses the y-axis is:
View SolutionStatement-1 : f(x) is a one-one function ⇔f−1(x) is a one-one function.
and
Statement-2 f−1(x) is the reflection of the function f(x) with respect to y = x.
View Solution
Knowledge Check
If f(x) is a linear function and f(2) = 1 and f(4) = -2 , then f(x) =
A−32x+4B32x−2C−32x+2D32x−4A linear function, f, has a slope of -2, f(1)=2 and f(2)=q. find q.
A0B32C52D3
The figure above shows the graph of the linear function, y=f(x). If slope of the line is -2 and f(3)=4, what is the value of b?A8B9C10D11
If f(x)=xx−1=1y then the value of f(y) is
View SolutionIf the graph of the function y=f(x) is as shown :

the graph of y=12(|f(x)|−f(x)) is
View SolutionTo find the point of contact P(x1,y1) of a tangent to the graph of y=f(x) passing through origin O, we equate the slope of tangent to y=f(x) at P to the slope of OP. Hence we solve the equation f'(x)=f(x1)x1 to get x1 and y1.Now answer the following questions (7 -9): The equation |lnmx|=px where m is a positive constant has a single root for
View SolutionLet f(x)=ax(a>0) be written as f(x)=f1(x)+f2(x), where f1(x) is an even function and f2(x) is an odd function. Then f1(x+y)+f1(x−y) equals :
View Solution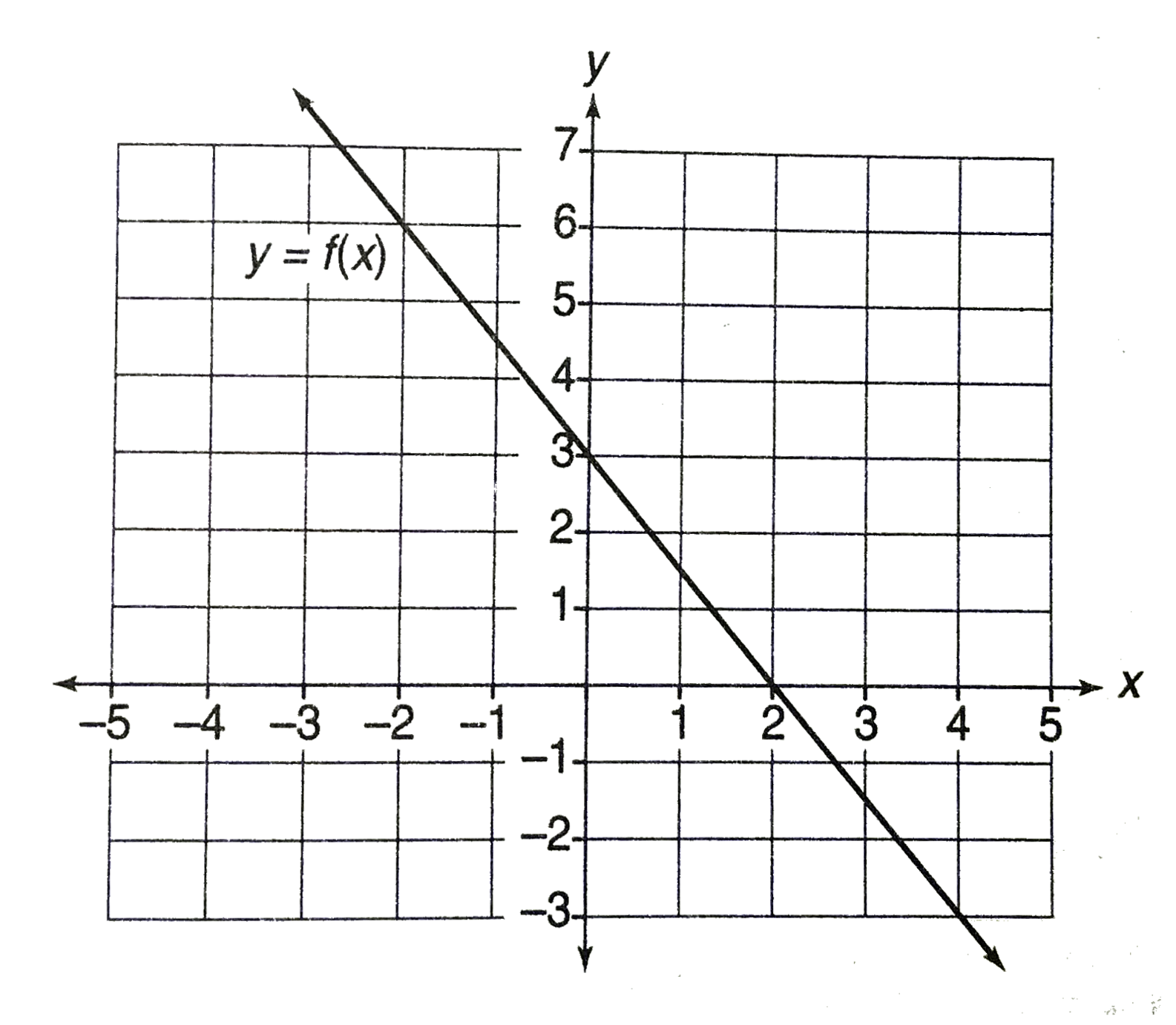
A linear function f is shown in the accompanying figure. If function g in the reflection of function f in the x-axis (not shown), what is the slope of the graph of function g?
View Solution

