If , then j =
64
81
The correct Answer is:C
To solve the equation 374√j−19=3717, we can follow these steps:
Step 1: Cross-Multiply
We start by cross-multiplying to eliminate the fractions:
37⋅17=37⋅(4√j−19)
Step 2: Simplify the Equation
Since 37 is common on both sides, we can cancel it out (assuming 37≠0):
17=4√j−19
Step 3: Isolate the Term with √j
Next, we add 19 to both sides to isolate the term with √j:
17+19=4√j
36=4√j
Step 4: Solve for √j
Now, we divide both sides by 4 to solve for √j:
√j=364
√j=9
Step 5: Square Both Sides
To find j, we square both sides:
j=92
j=81
Final Answer
Thus, the value of j is:
81
---
We start by cross-multiplying to eliminate the fractions:
37⋅17=37⋅(4√j−19)
Since 37 is common on both sides, we can cancel it out (assuming 37≠0):
17=4√j−19
Next, we add 19 to both sides to isolate the term with √j:
17+19=4√j
36=4√j
Now, we divide both sides by 4 to solve for √j:
√j=364
√j=9
To find j, we square both sides:
j=92
j=81
Thus, the value of j is:
81
Topper's Solved these Questions
- ALGEBRA Book:KAPLANChapter:ALGEBRA Exercise:ALGEBRA FOLLOW - UP TEST
Explore 10 Videos
- ADVANCED TECHINQUES FOR POLYNOMIALS AND RATIONAL EQUATIONSBook:KAPLANChapter:ADVANCED TECHINQUES FOR POLYNOMIALS AND RATIONAL EQUATIONSExercise:Multiple Choice Question
Explore 20 Videos
- CIRCLESBook:KAPLANChapter:CIRCLESExercise:Multiple Choice Question
Explore 12 Videos
Similar Questions
Compare the following fractions by using the symbol > or < or = :
(i) 3741 and1930 (ii) 1715 and119105
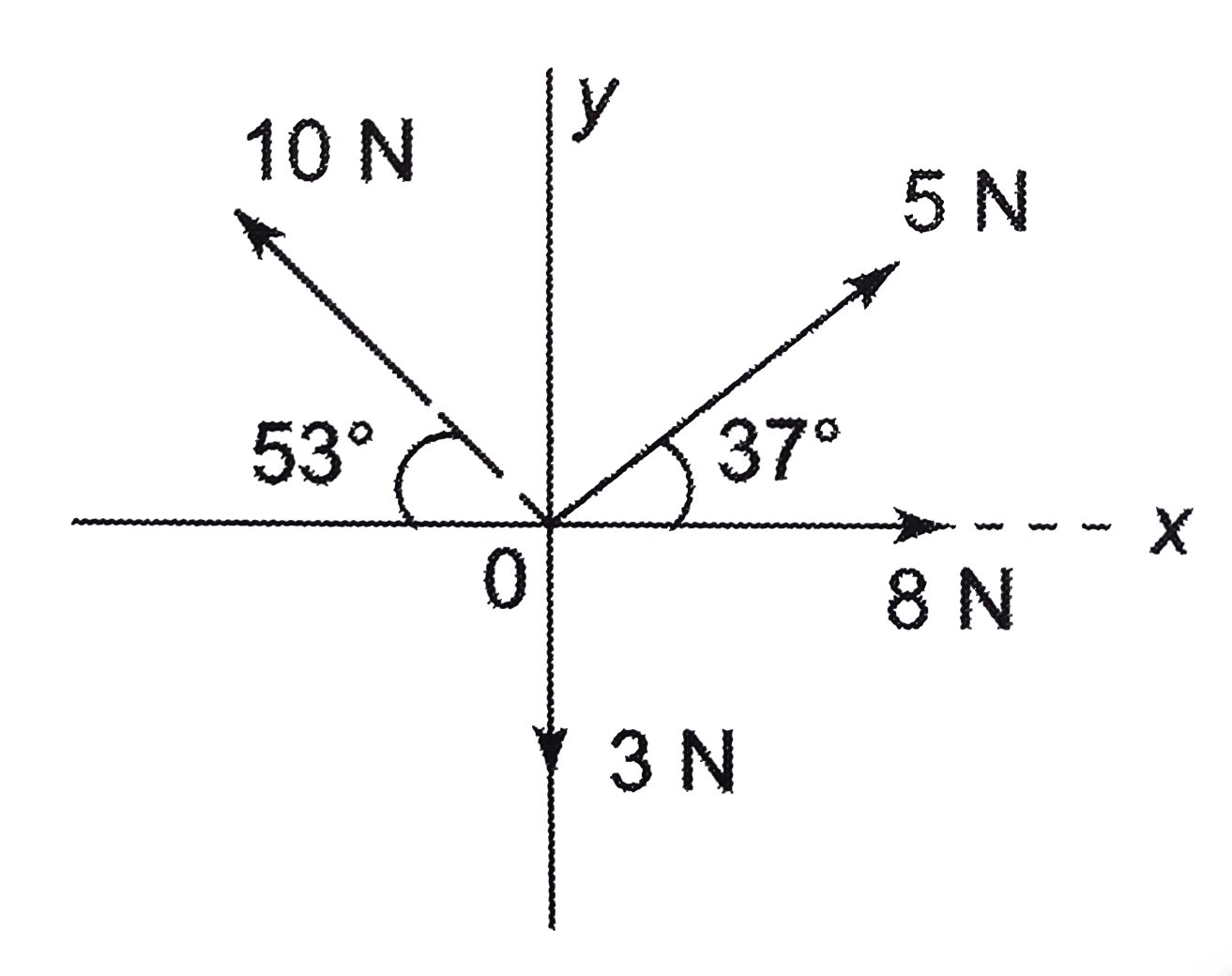
View SolutionFind the resultant of the following forces.
[sin37∘=35,cos37∘=45,sin53∘=45,cos53∘=35]
View SolutionIf N is a prime number which divides S=39P19+38P19+37P19+…+20P19, then the largest possible value of N among following is
View SolutionLet aj=74(23)j−1,j∈N. lf bj=a2j+aj, sum of the infinite sereies formed by bj's is (10+α) where [1α] is equal to ([] represent greatest integer function)
View SolutionThe coordinates of the foot of the perpendicular from the point (2,3) on the line −y+3x+4=0 are given by (3710,−110) (b) (−110,3710) (1037,−10) (d) (23,−13)
View SolutionThe coordinates of the foot of the perpendicular from the point (2,3) on the line −y+3x+4=0 are given by (a)(3710,−110) (b) (−110,3710) (c)(1037,−10) (d) (23,−13)
View SolutionDistance between line r=i+j+k+λ(2i+j+4k) and plane r.i+2j−k=3 is (1)4√6 (2) 5√6 (3) 1√6 (4)0(5) 2√6
View SolutionA non-zero vector →a is such that its projections along vectors ˆi+ˆj√2,−ˆi+ˆj√2 and ˆk are equal, then unit vector along →a is a.√2ˆj−ˆk√3 b. ˆj−√2ˆk√3 c. √2√3ˆj+ˆk√3 d. ˆj−ˆk√2
View SolutionFind the angle between the following pairs of lines: →r=λ(ˆi+ˆj+2ˆk) and →r=2ˆj+μ[(√3−1)ˆi−(√3+1)ˆj+4ˆk].
View SolutionThe unit vector which is orthogonal to the vector 3ˆj+2ˆj+6ˆk and is coplanar with vectors 2ˆi+ˆj+ˆkandˆi−ˆj+ˆk is 2ˆi−6ˆj+ˆk√41 b. 2ˆi−3ˆj√13 c. 3ˆj−ˆk√10 d. 4ˆi+3ˆj−3ˆk√34
View Solution

