Find the speed of the ring as a function of 'θ' if rope is pulled down with constant speed u:-
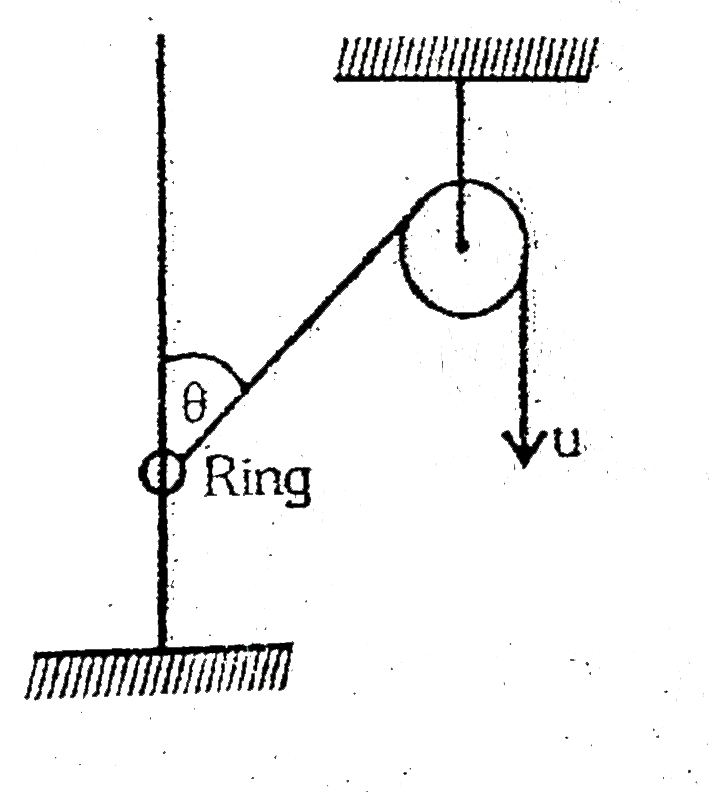
usinθ
ucosθ
u2sinθ
u2cosθ
The correct Answer is:B
Let speed of ring he v then vcosθ=u⇒v=ucosθ (∵ Magnitude of velocity along the string of any two points on string is same.)
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PAPER 2
60 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PAPER 3
100 Videos
- TEST PAPER 4BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS
45 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
Knowledge Check
In the arrangement of rigid links of equal length l, they can freely rotate about the joined ends as shown in the figure- 1.138. If the end U is pulled horizontally with constant speed 20 m/s, find the approx. speed of end P when the angle SUT is 90∘.
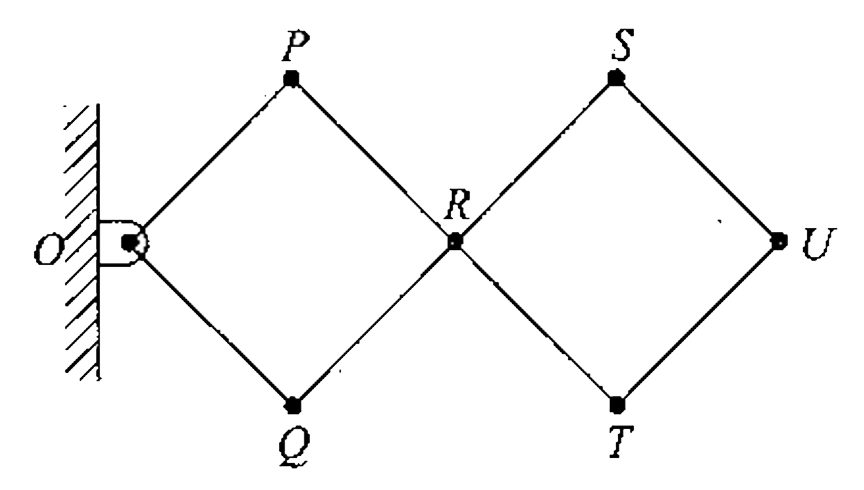A5 m/sB10 m/sC7.1 m/sD14.12 m/sA block of mass (m) slides along the track with kinetic friction mu. (A) man pulls the block through a rope which makes an angle θ with the horizontal as shown in the figure. The block moves with constant speed v. Power dlivered by man is
. ATvBTvcosθC(Tcosθ−μmg)vDzero
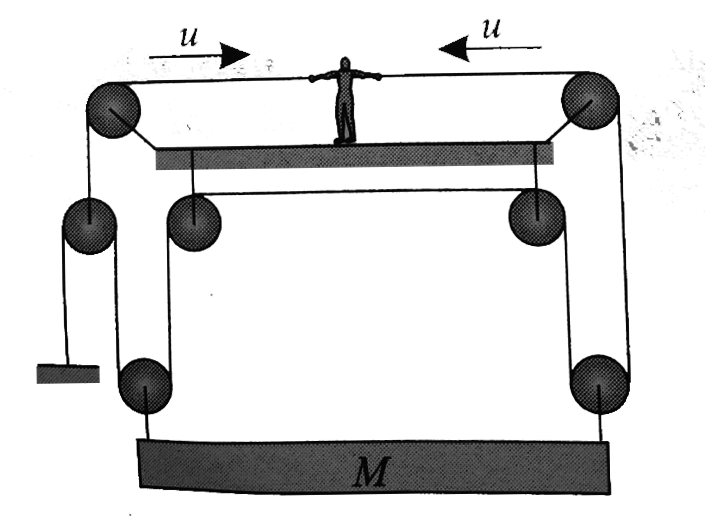
System is shown in the figure and man is pulling the rope from both sides with constant speed u find the speed of the block.
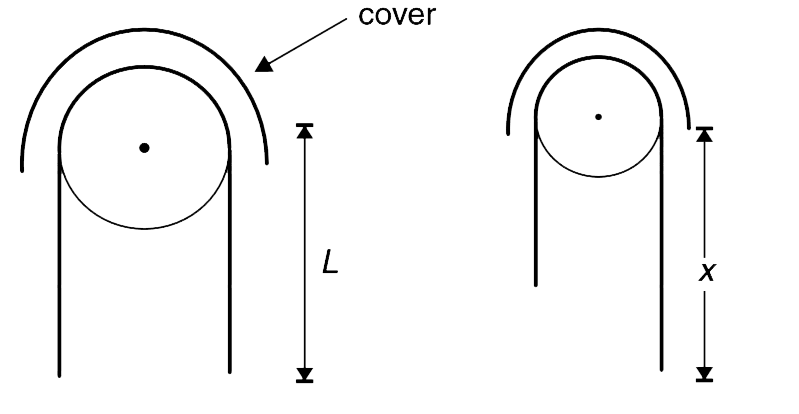
View SolutionA heavy rope of mass m and length 2L is hanged on a smooth little peg with equal lengths on two sides of the peg. Right part of the rope is pulled a little longer and released. The rope begins to slide under the action of gravity. There is a smooth cover on the peg (so that the rope passes through the narrow channel formed between the peg and the cover) to prevent the rope from whiplashing.
(a) Calculate the speed of the rope as a function of its length (x) on the right side.
(b) Differentiate the expression obtained in (a) to find the acceleration of the rope as a function of x.
(c) Write the rate of change of momentum of the rope as a function of x. Take downward direction as positive
(d) Find the force applied by the rope on the peg as a function of x.
(e) For what value of x, the force found in (d) becomes zero? What will happen if there is no cover around the peg ?
View SolutionA block of mass M is placed on a horizontal smooth table. It is attached to an ideal spring of force constant k as shown. The free end of the spring is pulled at a constant speed u. Find the maximum extension (x0) in the spring during the subsequent motion.
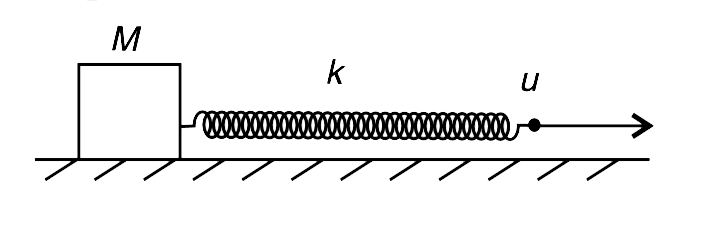
View SolutionA helicopter files horizontally with constant velocity in a direction θ east of north between two points AandB, at distance d apart. Wind is blowing from south with constant speed u, the speed of helicopter relative to air is nu where n>1. find the speed of the helicopter along AB. The helicopter returns from B to A with same speed nu relative to air in same wind. Find the total time for the journeys.
.
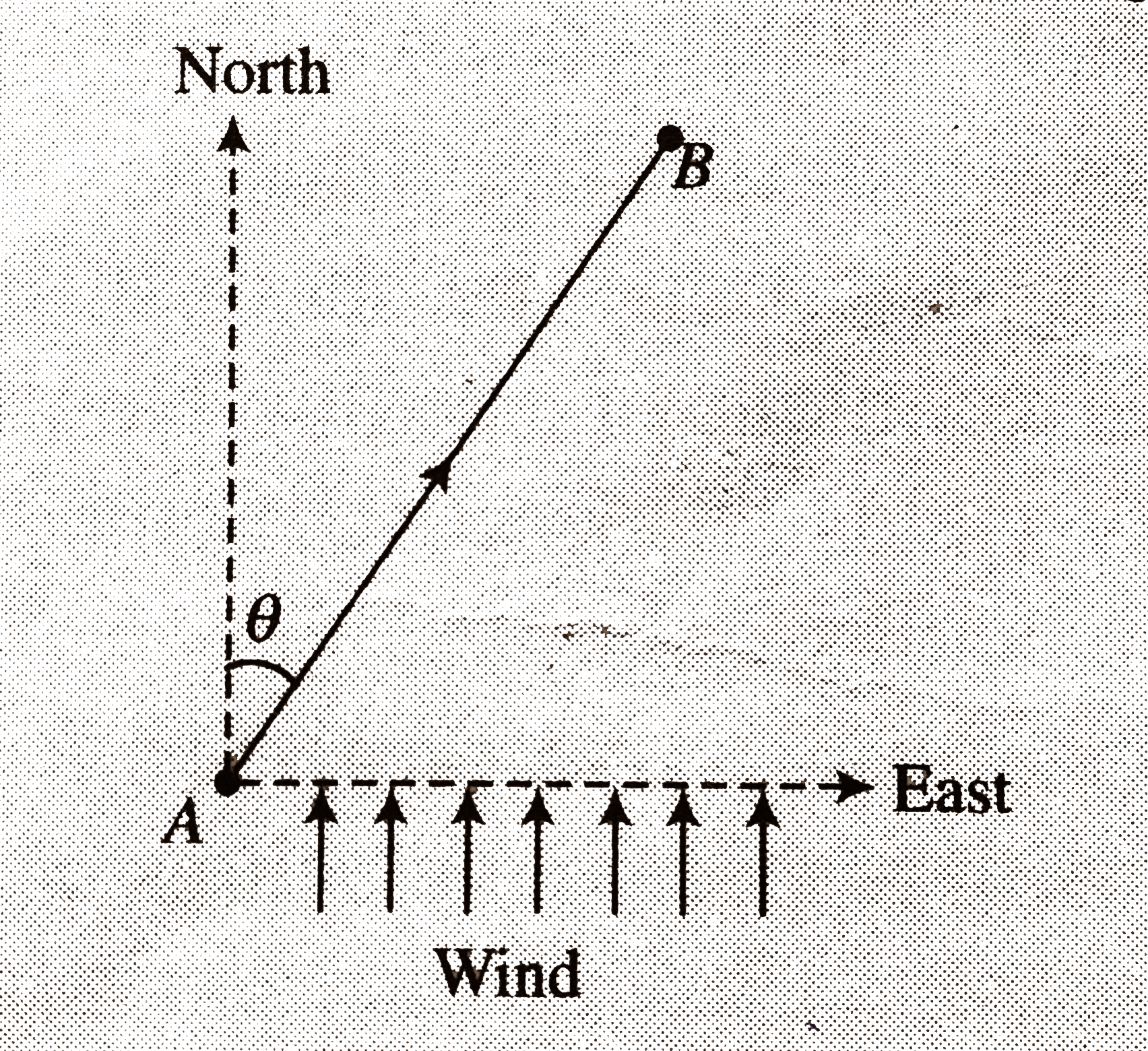View SolutionA ring of mass M and radius R lies flat on a horizontal table. A light thread is wound around it and its free end is pulled with a constant velocity v.
(a) Two small segment A and B (see fig.) in the ring are rough and have a coefficient of friction μ with the table. Rest of the ring is smooth. Find the speed with which the ring moves.
(b) Find the speed of the ring if coefficient of friction is μ everywhere, for all points on the ring.
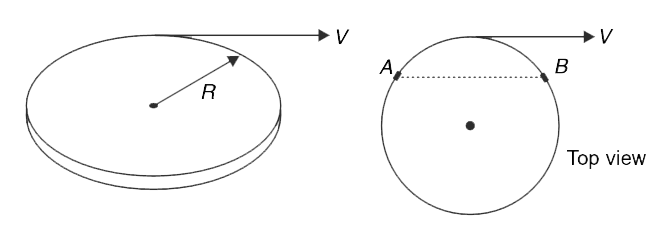
View SolutionA skier is pulled by towrope up frictionless ski slope that makes an angle of 12∘ with the horizontal . The rope moves parallel to the slope with a constant speed of 1.0 m/s. The force of the rope does 880 J of work on the skier as the skier moves a distance of 7.0 m up the incline. (a) If the rope moved with a constant speed of 2.0 m/s, how much work would the force of the rope do on the skier as the skier moved a distance of 8.0 m up the incline ? At what rate is the force of the rope doing work on the skier when the rope moves with a speed of (b) 1.0 m/s and (c) 2.0 m/s ?
View Solution