Question

Find the area of the region bounded by the ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$

Explanation

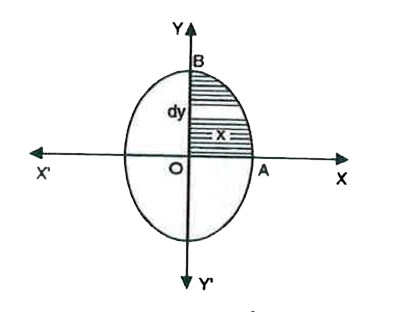
To find ,Area Enclosed by ellipse

Here, Ellipse is symmetrical about both x-axis and y-axis`therefore` Area of ellipse` =4 times Area of O A B`


`=4 times int_{0}^{a} y d x`


It is known that,



`frac{x^{2}}{a^{2}}+frac{y^{2}}{b^{2}}=1 `

`frac{y^{2}}{b^{2}}=1-frac{x^{2}}{a^{2}}`


`frac{y^{2}}{b^{2}}=frac{a^{2}-x^{2}}{a^{2}}`

`y^{2}=frac{b^{2}}{a^{2}}(a^{2}-x^{2})`




`y=pm sqrt{frac{b^{2}}{a^{2}}(a^{2}-x^{2})}`



`y=pm frac{b}{a} sqrt{(a^{2}-x^{2})}`


`Since` O A B is in 1^st quadrant, value of y is positive


`therefore` ` y=frac{b}{a} sqrt{a^{2}-x^{2}}`


Area of ellipse `=4 times int_{0}^{a} y cdot d x`


`=4 int_{0}^{a} frac{b}{a} sqrt{a^{2}-x^{2}} d x`


`=frac{4 b}{a} int_{0}^{a} sqrt{a^{2}-x^{2}} d x`



`sqrt{a^{2}-x^{2}} d x=frac{1}{2} x sqrt{a^{2}-x^{2}}+frac{a^{2}}{2} sin ^{-1} frac{x}{a}+c
=frac{4 b}{a}[frac{x}{2} sqrt{a^{2}-x^{2}}+frac{a^{2}}{2} sin ^{-1} frac{x}{a}]_{0}^{a}`

`=frac{4 b}{a}[(frac{a}{2} sqrt{a^{2}-a^{2}}+frac{a^{2}}{2} sin ^{-1} frac{a}{a})-(frac{0}{2} sqrt{a^{2}-0}-frac{a^{2}}{2} sin ^{-1}(0))]`

`=frac{4 b}{a}[0+frac{a^{2}}{2} sin ^{-1}(1)-0-0]`




`=frac{4 b}{a} times frac{a^{2}}{2} sin ^{-1}(1)`

`=2 a b times sin ^{-1}(1)`

`=2 a b times frac{pi}{2}`

`=pi a b`


`therefore` Required Area `=pi a b `square units