Write sufficient conditions for a point x=c to be a point of local maximum.
We know that at the extreme points of a function f(x), the first order derivative of the function is equal to zero, i.e.
f′(x)=0 at x=c
⇒f′(c)=0
Also, at the point of local maximum, the second order derivative of the function at the given point must be less than zero, i.e.
f′'(c)<0
Topper's Solved these Questions
Similar Questions
Knowledge Check
The sufficient conditions for the function f,R→R to be maximum at x=a will be
Af'(a)>0andf''(a)>0Bf'(a)=0andf''(a)=0Cf'(a)=0andf''(a)<0Df'(a)>0andf''(a)<0
If a∈(a1,a2) is the complete set satisfying the condition that the. point of local minima and the point of local maxima is less than 4 and greater than -2, respectively for the function f(x)=x3−3ax2+3(a2−1)x+1, then (a2−a1) is
View SolutionExamine the graph of following functions in each case identify the points of global maximum /minimum and local maximum /minimum.
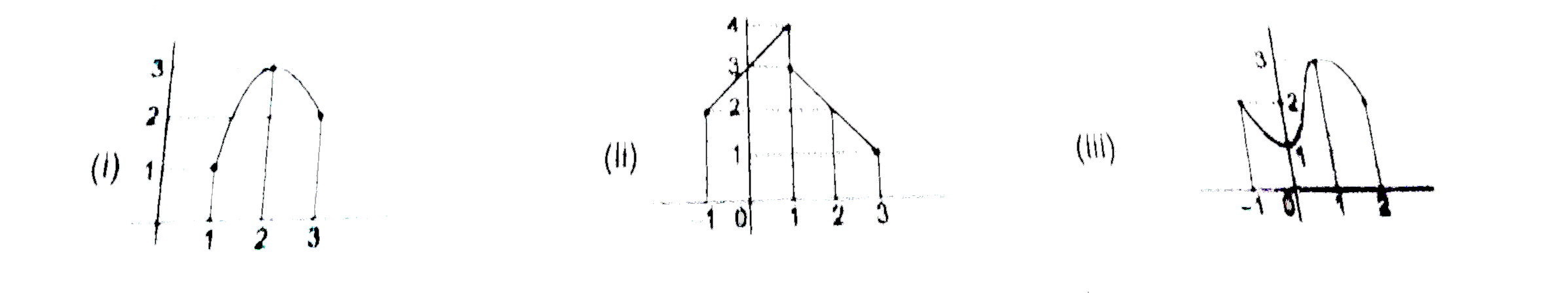
View SolutionConsider the function f(x)=(x−1)2(x+1)(x−2)3. What is the number of points of local minima of the function f(x)? What is the number of points of local maxima of the function f(x)?
View SolutionThe function f(x)=∣∣x2−2∣∣|x2−4| has, (a) no point of local maxima (b) no point of local minima (c) exactly one point of local minima (d) exactly one point of local maxima
View Solutionif limh→0[f(a−h)f(a)]=c where f(x) is a continuous function such that f(x)>0 for all x∈R and [.] denotes greatest integer function then which of the following statements is always true ? (A) If x=a is a point of local minima then c∈N (B) if x = a is a point of local maxima then c∈N (C) If x=a is a pioint of local minima then c∈I (D) If x=a is a point of local maximka then c∈I
View SolutionFind the points of local maxima or local minima and the corresponding local maximum and minimum values of each of the following functions:
f(x)=x2
View SolutionFind the points of local maxima or local minima and the corresponding local maximum and minimum values of each of the following functions:
f(x)=(x−3)4
View Solution

