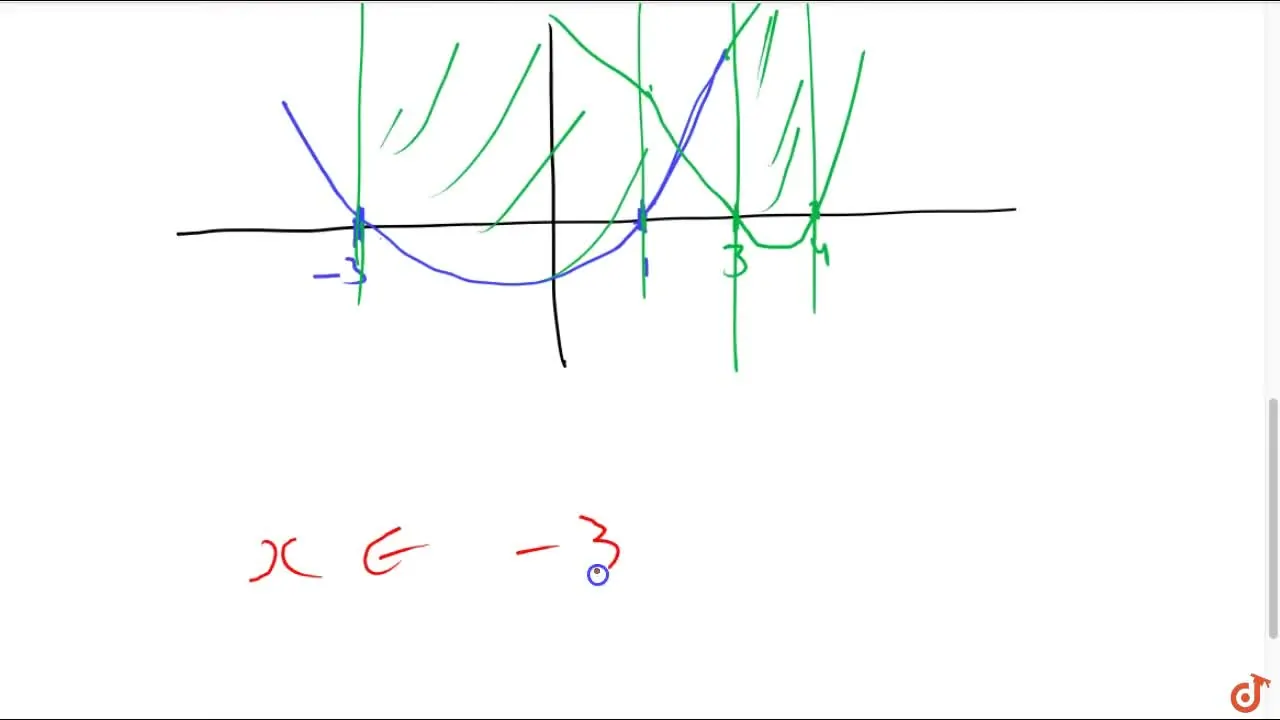
Solve: x2−4x+7x2−7x+12≤23 .
Video Solution
Text Solution
Given,x2−4x+7x2−7x+12≤23
=3x2−12x+21≤2x2−14x+24
=x2+2x−3≤0
=x2+3x−x−3≤0
=(x+3)(x−1)≤0
Thus x≤−3 and x≤1
|
Updated on:21/07/2023
Related Playlists
Similar Questions
Solve: x2−4x+7x2−7x+12≤23 .
View SolutionSolve:x2−4x+7x2−7x+12≤23.
View SolutionSolve(x2−x−1)(x2−x−7)<−5
View SolutionSolve (7x2+3x+8)+(4x2−5x+11)
View SolutionSolve 2x2−7x+3=0
View SolutionSolve 32x2−7x+7=9.
View SolutionSolve : 2(5x−7)≥3(4x−5)
View SolutionSolve: 3x2+5=7x
View SolutionSolve : 5x−23<4x−72
View SolutionSolve √3x2−7x−30+√2x2−7x−5=x+5.
View Solution