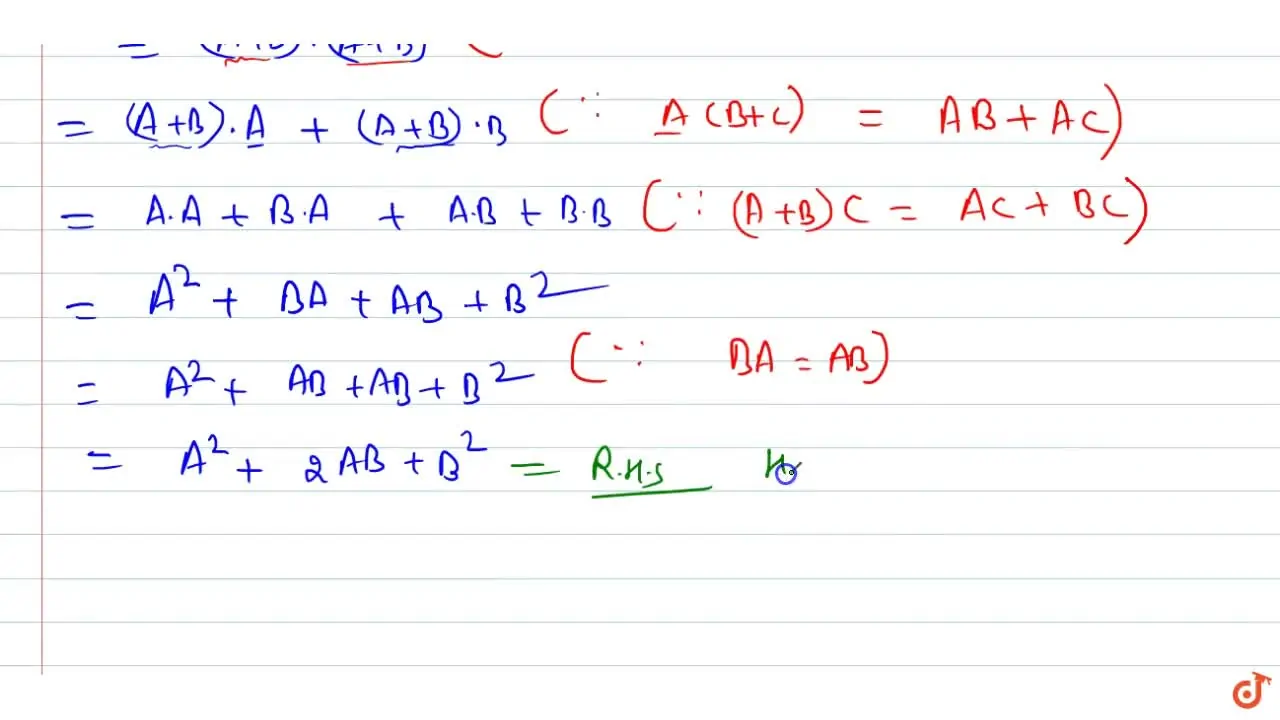If A and B are square matrices of the same order such that AB=BA , then show that (A+B)2=A2+2AB+B2 .
Video Solution
Text Solution
(A+B)2=(A+B)(A+B)
=A2+AB+BA+B2
=A2+AB+AB+B2
=A2+2AB+B2
|
Updated on:21/07/2023
Related Playlists
Similar Questions
If A and B are square matrices of the same order such that AB=BA , then show that (A+B)2=A2+2AB+B2 .
View SolutionIf A and B are square matrices of the same order such that AB=BA , then show that (A+B)2=A2+2AB+B2
View SolutionIf A and B are square matrices of the same order such that B = -A−1 BA , then (A+B)2 :
View SolutionIf A and B are square matrics of the same order then (A−B)2=?
View SolutionIf A and B are square matrics of the same order then (A+B)2=?
View SolutionIf A and B are square matrices of order 3, then
View SolutionIf A and B are square matrices of same order, then
View SolutionIf AandB are square matrices of the same order such that (A+B)(A−B)=A2−B2, then (ABA−1)2=
View SolutionIf A and B are two square matrices of the same order, then A+B=B+A.
View SolutionIf A and B are square matrics of the same order then (A+B)(A-B)=?
View Solution