Let g(x)=1+x−[x]andf(x)={−1,x<00,x=0f,x>0 . Then for all x,f(g(x)) is equal to (where [.] represents the greatest integer function). x (b) 1 (c) f(x) (d) g(x)
Video Solution
Text Solution
Correct option is B)
(1) When x>(−1)
then,
g(x)=1+x−[x]
=1+x−(−1)
=2+x
So,
f(g(x))=f(2+x)
=1+2+x−[2+x]
=3+x−2−x
=1
f(g(x))=1
(2)x=0
⇒f(g(x))=f(1+x−[x])
=1+1+x−[x]−[1+x−[x]]
=2+0−0−1−0+0
f(g(x))=1
(3)x>1
f(g(x))=f(1+x−[x])
=f(1+x−1)
=f(x)
=1
f(g(x))=1
Hence, f(g(x))=1 for all the classes.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Let g(x)=1+x−[x]andf(x)=⎧⎪⎨⎪⎩−1,x<00,x=01,x>0, then for all x,f[g(x)] is equal to
A0B1CxDf(x)Let g(x)=1+x-[x] and
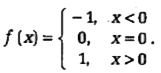Then for all x,f {g(x)} is equal to AxB1Cf(x)Dg(x)If f(x)=Sgn x and g(x)=1+x-[x], then for all x, f(g(x)) is equal to :
A0B1CxDf(x)
Let f(x)=∣∣∣(x+12)[x]∣∣∣,when −2≤x≤2∣. where [.] represents greatest integer function. Then
View SolutionLet g(x) = 1 + x – [x] and f(x)=⎧⎪⎨⎪⎩−1ifx<00ifx=01ifx>0 then Aax,fog(x) equals
(where [ * ] represents greatest integer function).
View SolutionLet f(x)=|x|andg(x)=[x], (where [.] denotes the greatest integer function) Then, (fog)'(−1) is
View SolutionIf f(x)={1−|x|1+xx≠−11x=−1, then f([2x]) is (where [*] represent greatest integer function)
View Solutioniff(x)={1−|x|1+xx≠−11x=−1then f([2x]) , where [.] represents the greatest integer function , is
View Solution