Distinguish between
(a) Glycine and acetamide
(b) α−,β− & γ− amino acids.
Video Solution
Text Solution
The correct Answer is:(a) By NaHCO3 (By ninhydrin test)
(b)(##RESORGCHMV02XIIC04E01122_A01##)
The following reaction are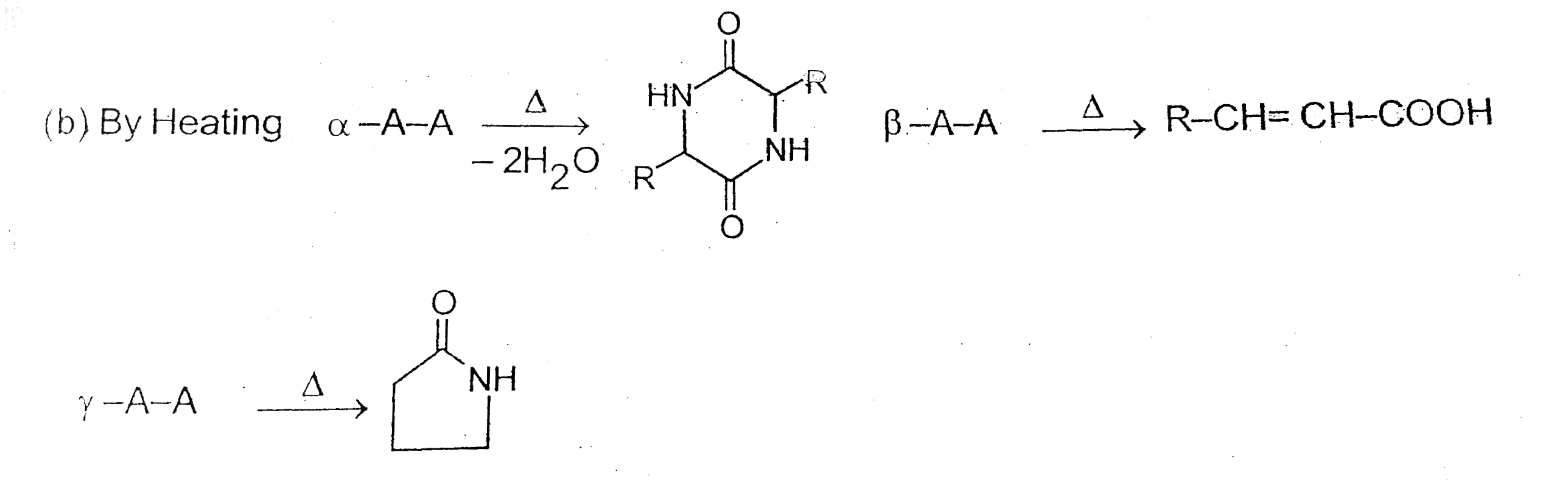
|
Topper's Solved these Questions
- BIOMOLECULESBook:RESONANCEChapter:BIOMOLECULESExercise:Ex-2(Single correct)Part-II
Explore 17 Videos
- BIOMOLECULESBook:RESONANCEChapter:BIOMOLECULESExercise:Ex-2(More correct)Part-II
Explore 14 Videos
- BIOMOLECULESBook:RESONANCEChapter:BIOMOLECULESExercise:Ex-1(Assertion/Reasoning)Part-III
Explore 10 Videos
- BASIC CONCEPTSBook:RESONANCEChapter:BASIC CONCEPTSExercise:ORGANIC CHEMISTRY(BASIC CONCEPTS)
Explore 27 Videos
- BIOMOLECULES & POLYMERBook:RESONANCEChapter:BIOMOLECULES & POLYMERExercise:ORGANIC CHEMISTRY(Biomolecules & Polymer)
Explore 33 Videos
Similar Questions
Knowledge Check
sin(β+γ−α)+sin(γ+α−β)+sin(α+β−γ)−sin(α+β+γ)=
A2sinαsinβsinγB4sinαsinβsinγC8sinαsinβsinγDsinαsinβsinγArrange in increasing order of:
a. The mass of α,β, and γ
b. The penetration power of α,β, and γ
c. The speed of α,β, and γ
d. The inoization capacity of gases of α,β, and γAThe mass of α β and γBThe penetration of α β and γCThe speed of α β and γDThe ionization capacity of gases of α β and γAssertion (A) All naturally occurring α-aminoacids except glycine are optically active.
Reason (R) Most naturally occurring amino acids have L-configuration.AAssertion and reason both are correct statements and reason explains the assertion.BBoth assertion and reason are wrong statements.CAssertion is correct statement and reason is wrong statement.DAssertion and reason both are correct statements but reason does not explain assertion.
sin(β+γ−α)+sin(γ+α−β)+sin(α+β−γ)−sin(α+β+γ)=
View Solutioncos(α+β)cosγ−cos(β+γ)cosα=sinβsin(γ−α)
View SolutionDo the following conversions.
Acetic acid to glycine (α- amino acetic acid)
View SolutionIf f(x)=∣∣ ∣ ∣∣cos(x+α)cos(x+β)cos(x+γ)sin(x+α)sin(x+β)sin(x+γ)sin(β+γ)sin(γ−α)sin(α−β)∣∣ ∣ ∣∣, then (Given α≠β≠γ)
View SolutionIf α,βandγ are the roots of the equation x3+x+2=0, then the equation whose roots are (α−β)(α−γ),(β−γ)(β−γ)and(γ−α)(γ−α) is
View Solution