A neutron of kinetic $6.5 e V$ collides inelastically with a singly ionized helium atom at rest. It is scattered at an angle $90^{\circ}$ with respect to its original direction.
Find the maximum allowed value of energy of the He atom?

Video Solution

Text Solution

Verified by Experts

The correct Answer is:(a) $6.36 e V, 0.312 e V$ (of neutron), $17.84 e V, 16.328 e V$ (of atom)
(b) $1.82 \times 10^{15} H z, 11.67 \times 10^{15} H z, 9.84 \times 10^{15}$

Let $K_{1}$ and $K_{2}$ be the kinectic energies of neutron and helium atom after collision and $Δ E$ be the excitation energy

From conservation of linear momentum along x-direction.
$\Rightarrow \sqrt{2 K m} = \sqrt{2 (4 m) K_{2}} cos θ (P = \sqrt{2 K m})$
Similarly.,applying conservation of linear momentum in y-direction, we have
$\sqrt{2 m_{1} m} = \sqrt{2 (4 m) K_{2}} sin θ$
Squaring and adding equation (1) and (2), we get
$K + K = 4 K_{2}$
or $4 K_{2} - K_{1} = K = 65 e V$
Now, during collision, electron cana be excited to any higher energy state. Applying conservation of energy we get $K = K_{1} + K_{2} + Δ$

or $65 = K_{1} + K_{2} + Δ E$
$Δ E$ can have the following values,
$Δ E_{1} = {- 13.6 - (- 54.4)} e V = 40.8 e V$
Substituting in $(5)$ , we get
$K_{1} + K_{2} = 24.2 e V$
Solving (4) and (6), we get
$K_{1} = 6.36 e V$ and $K_{2} = 17.84 e V$
Similarly, when we put $Δ E = Δ E_{2}$
${- 6.04 - (54.4)} e V$
in equation $(5)$ , we get
$K_{1} + K_{2} = 14 e V$
Now, solving $(4)$ and $(8)$ , we get
$K_{1} = - 1.8 e V$ and $K_{2} = 15.8 e V$
But since the Kinetic energies cannot have the values, the electron will not jump to third excited state of $n = 4$ .
Therefore, the allowed values of $K_{1}$ ( KE of neutron) are $6.36 e V$ and $0.312 e V$ and of $K_{2}$ (KE of the atom) are $17.84 e V$ and $16.238 e V$ and the electron can jump upto second exicted state only $(n = 3)$
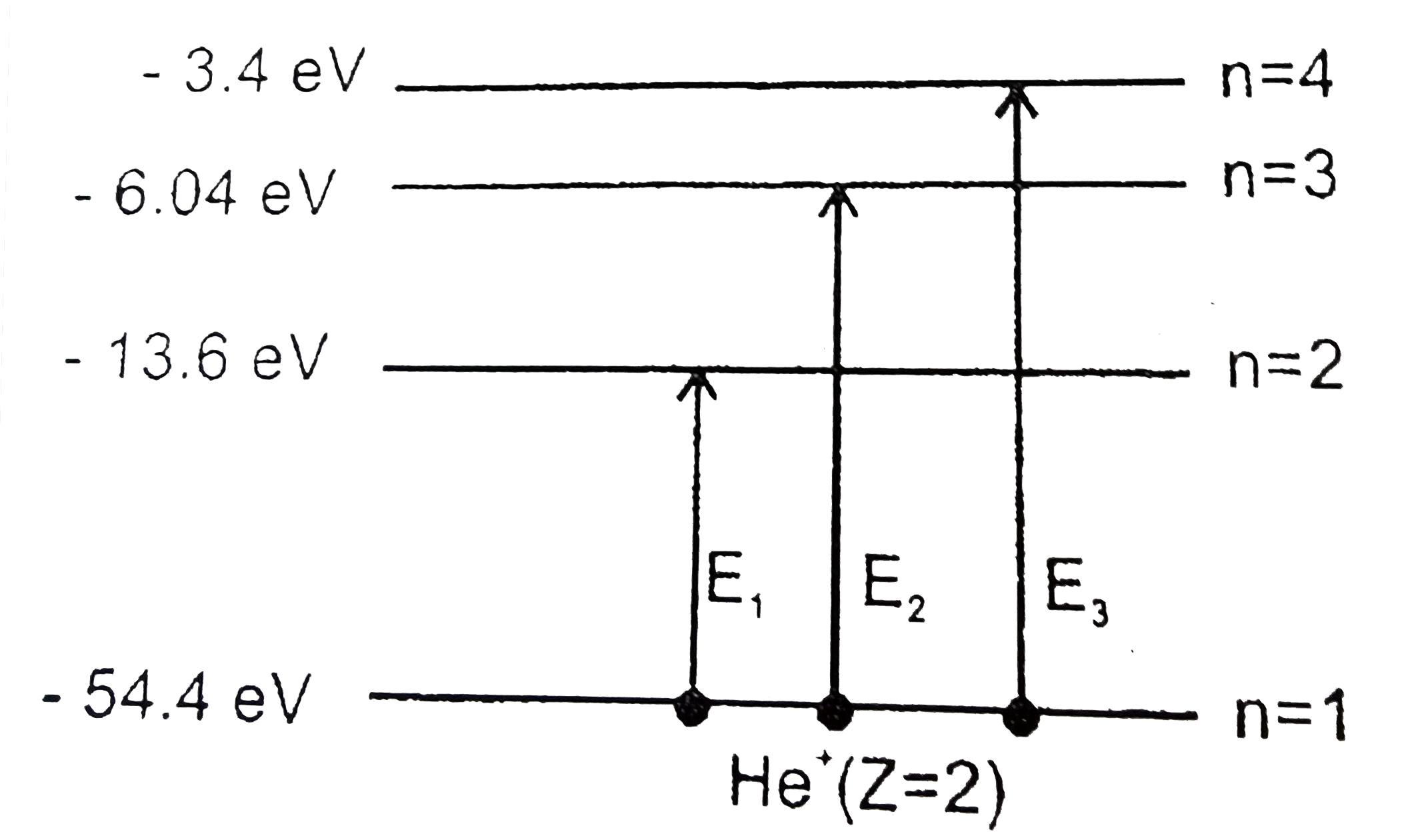
(b) Possible emission lines are only three as shown in figure. The correspinding frequencies are
$V_{1} = \frac{(E_{3} - E_{2})}{h}$
$= \frac{{- 6.04 - (- 13.6)} \times 1.6 \times 10^{- 19}}{6.63 \times 10^{- 34}} H z$
$= 1.82 \times 10^{15} H z$
$V_{2} = \frac{E_{2} - E_{1}}{h}$
$= \frac{{- 6.04 - (54.4)} \times 1.6 \times 10^{1 - 9}}{6.63 \times 10^{- 34}} H z$
$11.67 \times 10^{15} H z$
and $V_{3} = \frac{E_{2} - E_{1}}{h}$
$= \frac{{- 13.6 - (54.4)} \times 1.6 \times 10^{- 19}}{6.63 \times 10^{- 34}} H z$
$9.84 \times 10^{15} H z$
Hence, the frequencies of emitted radiations are $1.82 \times 10^{5} H z, 11.67 \times 10^{15} H z$ and $9.84 \times 10^{15} H z$ .

|

Updated on:21/07/2023

Class 12 PHYSICS ATOMS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A neutron of kinetic $6.5 e V$ collides inelastically with a singly ionized helium atom at rest. It is scattered at an angle $90^{\circ}$ with respect to its original direction.
Find the minimum allowed value of energy of the neutron.
A $0.39 e V$
B $0.32 e V$
C $0.25 e V$
D $0.43 e V$
Question 2 - Select One or More
A neutron having kinetic energy $E_{0}$ collides with singly ionised He atom at rest and move along initial direction. Which of the following statement(s) is/are true for the above mentioned collision.
ACollision will be perfectly inelastic if $E_{0} = 17 e V$
BCollision will be perfectly inelastic is $E_{0} = 8.16 e V$
CIf $E_{0} =$ then ploton of wavelength $λ = 500 m$ is observed just after the collision if $E_{0} = 8.16 e V$ .
DPerfectly elastic collision is not possible.
Question 3 - Select One
A neutron in a nuclear reactor collides head on elastically with the nucleus of a carbon atom initially at rest. The fraction of kinetic energy transferred from the neutron to the carbon atom is
A $\frac{11}{12}$
B $\frac{2}{11}$
C $\frac{48}{121}$
D $\frac{48}{169}$

RESONANCE-ATOMIC PHYSICS-Advanved level problems

Home
Ask Doubt
Profile