Consider the beta decay
^198Au→198Hg∗+Bη−1+→v.
where ^198Hg∗ represents a mercury nucleus in an excited state at energy 1.088MeV above the ground state. What can be the maximum kinetic energy of the electron emitted? The atomic mass of ^198Au is 197.968233u and that of ^198Hg is 197.966760u.
If the product necleus .198Hg is formed in its ground state, the kinetic energy available to the electron and the antineutrino is
Q=[m(.18Au)−m(.198Hg)]c2.
As .198Hg∗ has energy 1.088MeV more than .198Hg in gorund state, the kinetic energy actually available is
Q=[m(.198Au)−m(.198Hg)]c2−1.088MeV.
=(197.968233u−197.966760u)(931MeVu)−1.088MeV
=1.3686MeV−1.088MeV=0.2806MeV.
This is also the maximum possible kinetic energy of the electron emitted.
Topper's Solved these Questions
- NUCLEAR PHYSICSBOOK - RESONANCECHAPTER - NUCLEAR PHYSICSEXERCISE - Exercise -1 Part-1 Subjective questions
12 Videos
- NUCLEAR PHYSICSBOOK - RESONANCECHAPTER - NUCLEAR PHYSICSEXERCISE - Exercise-1 Part-2 Only one option correct type
27 Videos
- GRAVITATIONBOOK - RESONANCECHAPTER - GRAVITATIONEXERCISE - HIGH LEVEL PROBLEMS
16 Videos
- REVISION DPPBOOK - RESONANCECHAPTER - REVISION DPPEXERCISE - All Questions
444 Videos
Similar Questions
In beta decay, 10Ne23 is converted into 11Na23. Calculate the maximum kinetic energy of the electrons emitted, given atomic masses of 10Ne23 and 11Na23 arc 22.994466 u and 22.989770 u, respectively.
View SolutionFind the maximum energy that a beta particle can have in the following decay
^176Lu→176Hf+e+→v.
Alomic mass of ^176Lu is 175.942694u and that of ^176Hf is 175.941420u.
View Solution
Knowledge Check
During β-decay of stationary nucleus , an electron is observed with a kinetic energy 1.0 MeV . From this ,what can be concluded about the Q-value of the decay ?
AQ=1.0 MeVBQ≤1.0MeVCQ≥1.0MeVDNoting can be concluded about the Q-valueGold .19879Au undergoes β− decay to an excited state of .19880Hg. If the excited state decays by emission of a γ-photon with energy 0.412MeV, the maximum kinetic energy of the electron emitted in the decay is (This maximum occurs when the antineutrino has negligible energy. The recoil energy of the .19880Hg nucleus can be ignored. The masses of the neutral atoms in their ground states are 197.968255u for .19879Hg).
A0.412MeVB1.371MeVC0.959MeVD1.473MeV
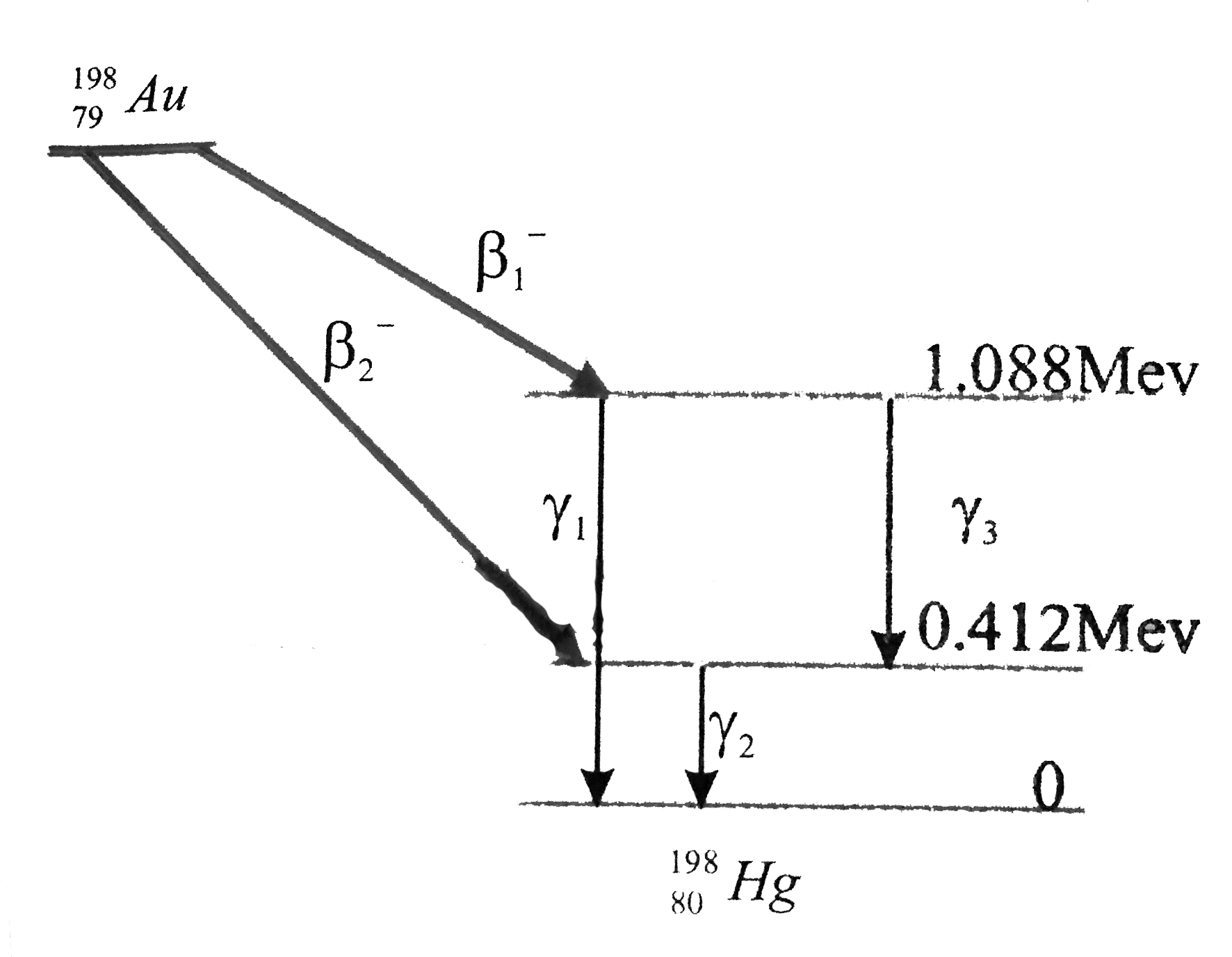
Obtain the maximum kinetic energy of β-particles, and the radiation frequencies of γ decays in the decay scheme shown in Fig. 14.6. You are given that m(.198Au)=197.968233u,m(.198Hg)=197.966760u
View SolutionThe isotope _(5)12B having a mass 12.014uundergoesβ−decay→126C126Chas an excited state of the nucleus (_(6)12C∗at4.041MeV above its ground state if _(5)12Edecay→126C∗ , the maximum kinetic energy of the β−partic≤in unit of MeVis(1u=931.5MeV/c2 where is the speed of light in vacume ) .
View SolutionCalculate the maximum kinetic energy of the bera particle emitted in the following decay scheme:
^12N rarr 12C∗+e++v
^12C rarr ^12C+γ(4.43MeV).
The atomic mass of 12Nis12.018612u.
View SolutionThe nucleus .23Ne decays by β-emission into the nucleus .23Na. Write down the β-decay equation and determine the maximum kinetic energy of the electrons emitted. Given,(m(.2311Ne)=22.994466amu and m(.2311Na=22.989770amu. Ignore the mass of antineutrino (¯v).
View SolutionNeon-23 decays in the following way,
_1023Ne→2311Na+0−1e+¯v
Find the minimum and maximum kinetic energy that the beta particle(_(−1)0e)can have. The atomic masses of ^23Ne and ^23Na are 22.9945u and 22.9898u, respectively.
View SolutionAn excited .69Z⋅n Nucleus at rest decays to ground state .69Zn by way of emitting a gamma photon. The energy equivalent of difference in mass of Z⋅n and Zn is 0.44 MeV. Calculate the kinetic energy of recol of Zn nucleus. Rest mass of .69Zn is M0=68.927u.
View Solution
