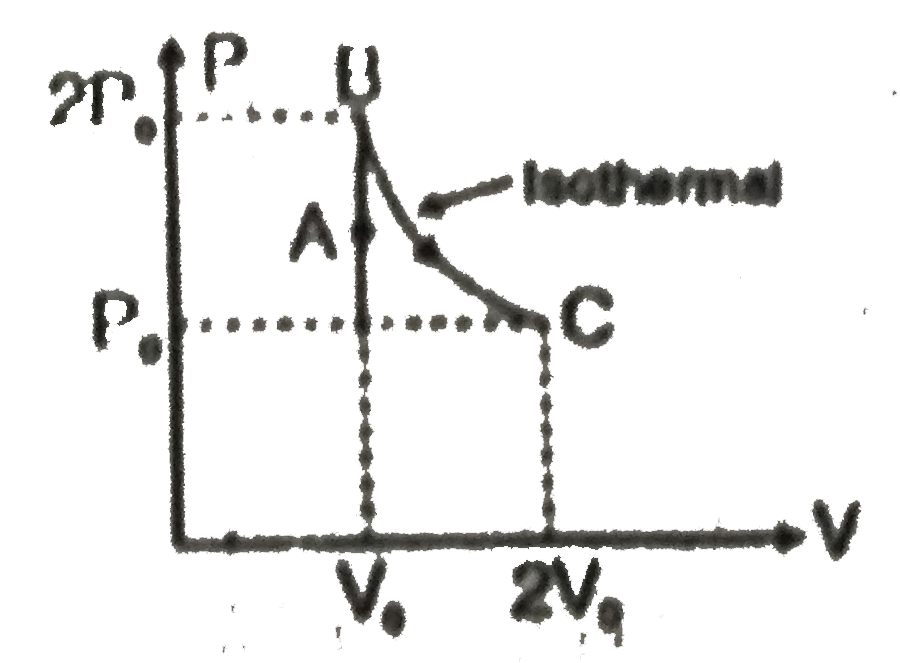
A diatomic ideal gas undergoes a thermodynamic change according to the P-V diagram shown in the figure. The total heat given to the gas is nearly ( use ln2=0.7):
A
2.5P0V0
B
1.4P0V0
C
3.9P0V0
D
1.1P0V0
Video Solution
Text Solution
The correct Answer is:C
QAB=ΔUAB+WAB
WAB=0
ΔUAB=f2nRΔT=f2(ΔPV)
ΔUAB=52(ΔPV)
QAB=2.5P0V0
Process BC,BC
QBC=ΔUBC+WBC
QBC=0+2P0V0ln2=1.4P9V0
Qnet=QAB+QBC=3.9P0V0

|
Topper's Solved these Questions
Similar Questions
Knowledge Check
A diatomic ideal gas undergoes a thermodynainic change according to the P-V diagram shown in figure, The total heat given to the gas is nearly
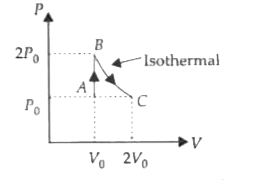 A2.5P0V0B1.4P0V0C3.9P0V0D1.1P0V0
A2.5P0V0B1.4P0V0C3.9P0V0D1.1P0V0A monoatomic ideal gas undergoes a process ABC. The heat given to the gas is
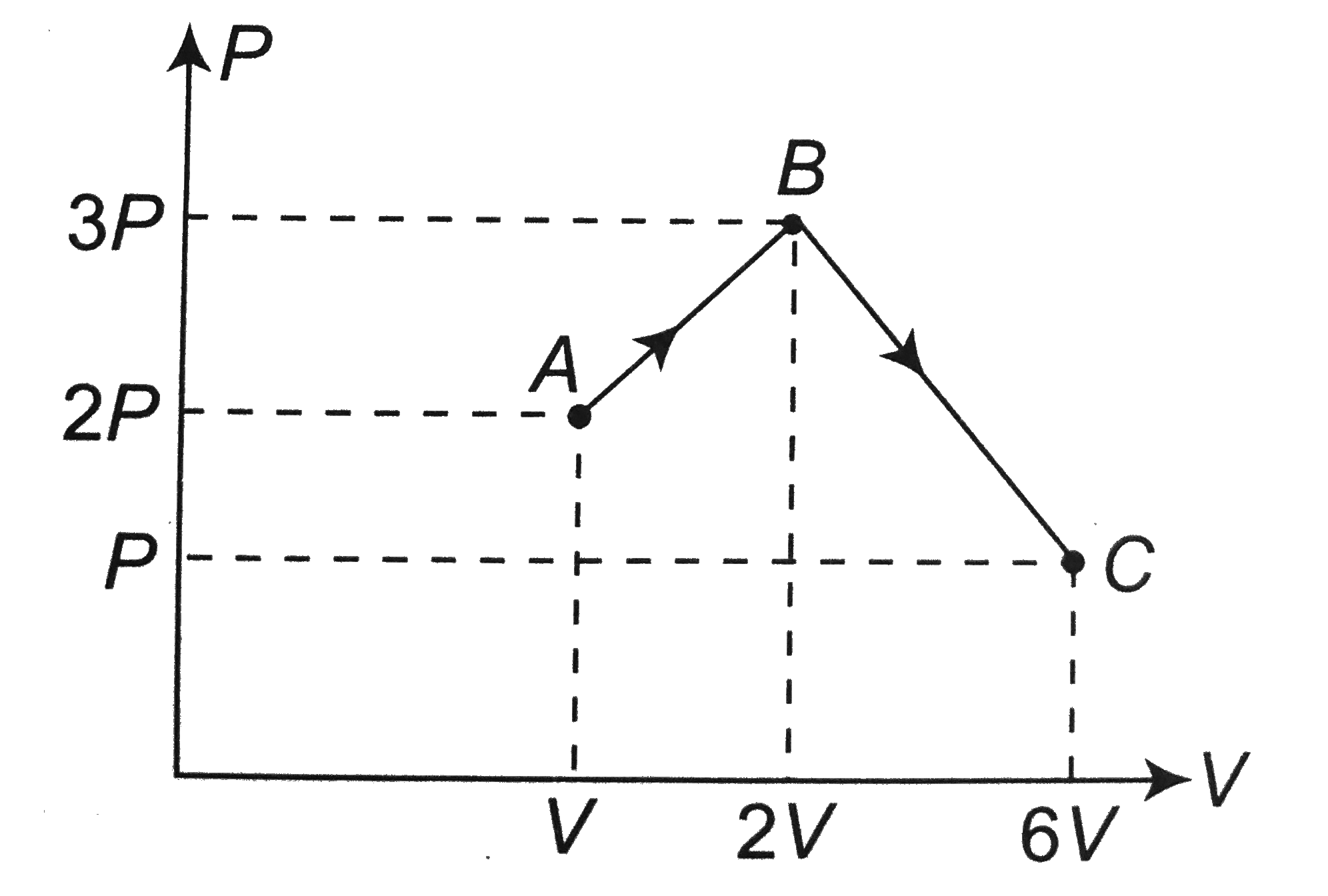 A7.5PVB12.5PVC16.5PVD20.5PV
A7.5PVB12.5PVC16.5PVD20.5PVOne mole of an ideal diatomic gas is taken through a process whose P−V diagram is shown in the figure. The work done by the gas is
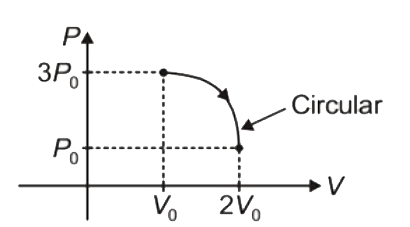 AπP0V0+2P0V0BπP0V02+P0V0C2πP0V0+P0V0DπP0V0√2+P0V0
AπP0V0+2P0V0BπP0V02+P0V0C2πP0V0+P0V0DπP0V0√2+P0V0
P-V curve of a diatomic gas is shown in the Fig. Find the total heat given to the gas in the process A→B→C

View SolutionAn ideal diatomic gas undergoes a thermodynamic process as shown in the P−V diagram. The process AB is isochoric while the process BC is isothermal. The total heat gain to the gas in the process is nearly (use ln2=0.7)
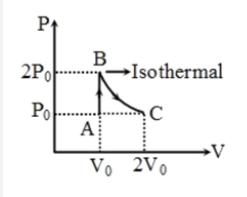
View SolutionOne mole of monatomic ideal gas undergoes the process A→B , as in the given P−V diagram . The specific heat for this process is

View SolutionOne mole of a diatomic gas undergoes a thermodynamic process, whose process equation is P∝V2. The molar specific heat of the gas is
View SolutionThe process in which an ideal gas undergoes change from X to Y as shown in the figure diagram is :
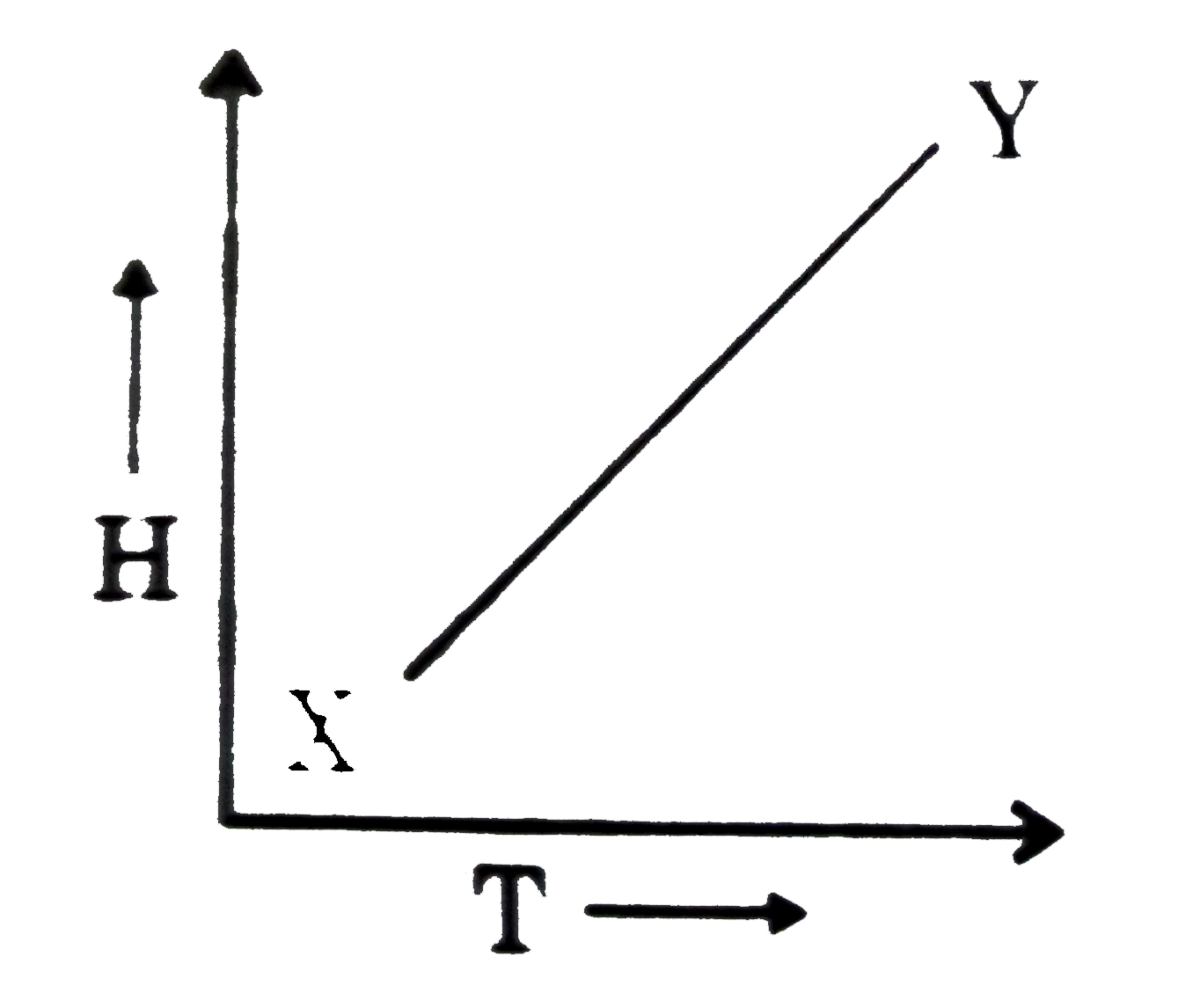
View Solution