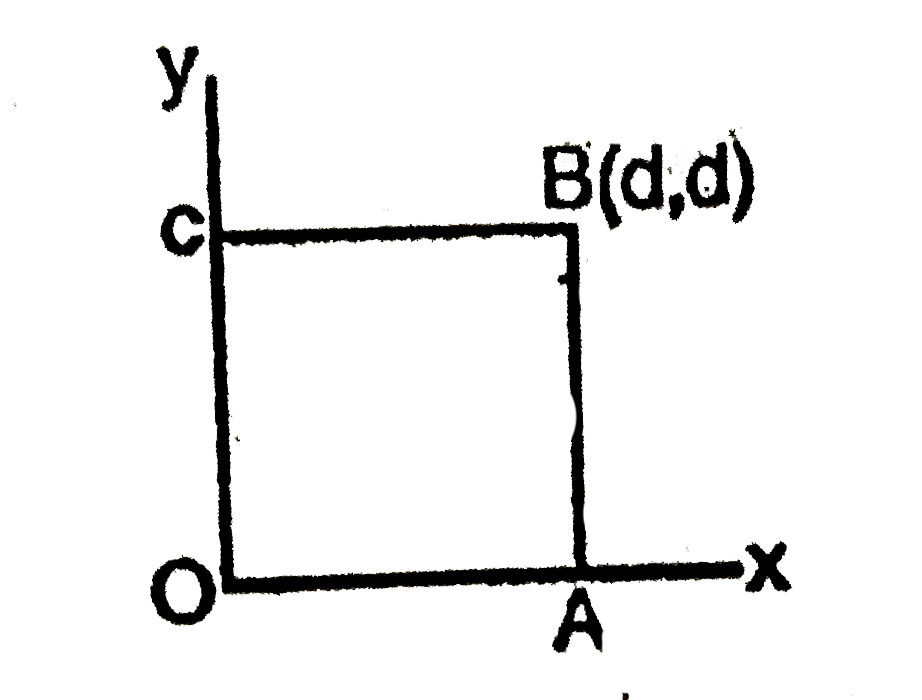
The work done by the force , where A is a constant and x & y are in meters around the path shown is :
zero
Ad
The correct Answer is:D
Topper's Solved these Questions
Similar Questions
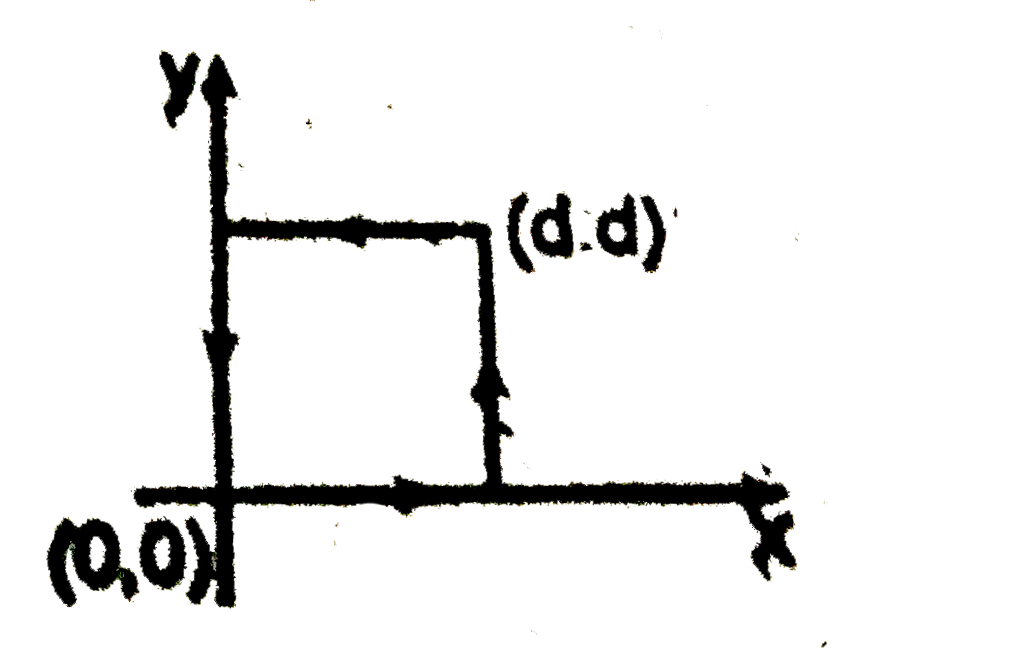
A particle moves in x-y plane from (0,0) to (a,a) and is acted upon by a force →F=k(y2ˆi+x2ˆj)N, where k is a constant and x and y are coordinates in meter. Find work done by this force, if the particle moves along
Two straight lines first from (0,0) to (a,0) and then from (a,0) to (a,a)
View SolutionThe electric field strength depends only on the x and y coordinates according to the law E = a(xˆi+yˆj)x2+y2 , where a is a constant ˆi and ˆj are unit vectors of the x and y axes . Find the potential difference between x = 1 and x = 5 :
View Solution
Knowledge Check
The work done by the forces →F=2ˆi−ˆj−ˆk in moving an object along the vectors 3ˆi+2ˆj−5ˆk is:
A−9 unitsB15 unitsC9 unitsDNone of theseWhat is the work done when a force →F=2ˆi+3ˆj−5ˆk units acts on a body, producing a displacement →S=2ˆi+4ˆj+3ˆk units ?
Azero unitsB30 unitsC1 unitD45 unitsThe work done by a force F=(ˆi+2ˆj+3ˆk) N ,to displace a body from position A to position B is [The position vector of A is r1=(2ˆi+2ˆj+3ˆk)m]
A5 JB3 JC2 JD10 J
A force →F=(−yˆi+xˆj)N acts on a particle as it moves in an anticlockwise circular motion in x-y plane. The centre of the circle is at the origin. If the work done by the force is 32πJ in one complete revolution then asSigmaing x,y to be in meters, find the radius of the path.
View SolutionThe intensity of an electric field depends only on the coordinates x and y as follows,
E=a(xˆi+yˆj)x2+y2 where, a is constant and ˆi and ˆj are the unit vectors of the x and y axes. Find the charges within a sphere of radius R with the centre at the origin.
View SolutionA particle is moved along the different paths OAC,OBC&ODC as shown in the figure . Path ODC is a parabola , y=4x2. Find the work done by a forc →F=xyˆi+x2y on the particle along these paths. Is this force a conservative force ?
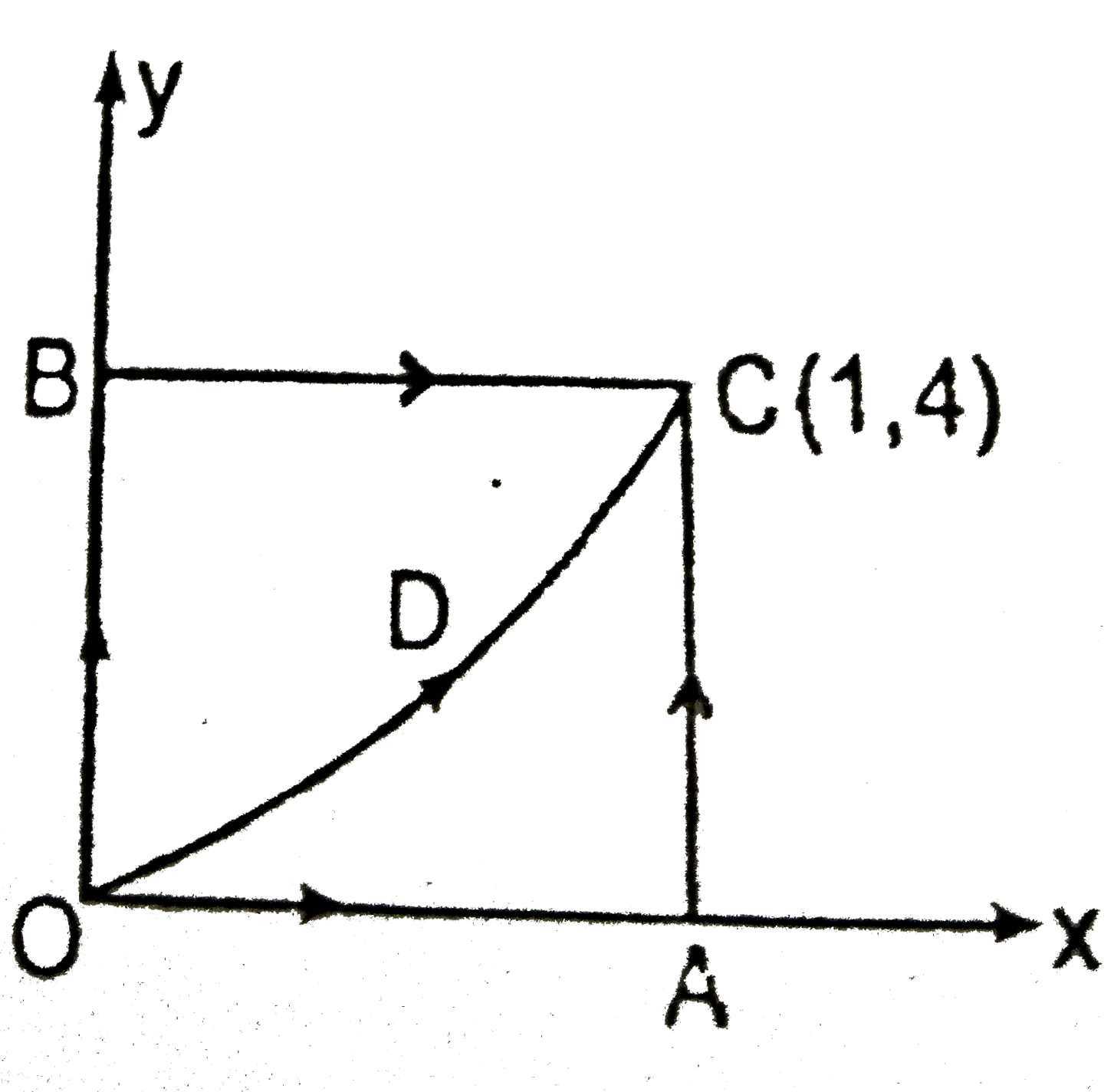
View SolutionA body is displaced from prigin to (1m,1m) by force
F=(2yˆi+3x2ˆj) along two paths
(a) x=y (b) y=x2
Find the work done along both paths.
View SolutionA force F=−K(yˆi+xˆj) (where K is a positive constant) acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0), and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
View Solution