A manufacturer of radio sets produced 600 units in the third year and 700 units in the seventh year. Assuming that the product increases uniformly by a fixed number every year, find i. the production in the first year ii. the total product in 7 years and iii. the product in the 10th year.
To solve the problem step by step, we will use the properties of Arithmetic Progressions (AP).
Given Information:
- Production in the 3rd year (A3) = 600 units
- Production in the 7th year (A7) = 700 units
- The production increases uniformly by a fixed number (d) each year.
Step 1: Establish the general formula for the nth term of an AP.
The nth term of an AP can be expressed as:
An=A+(n−1)⋅d
where:
- A = first term (production in the first year)
- d = common difference (increase in production each year)
Step 2: Write equations for A3 and A7.
Using the formula for the nth term, we can write:
1. For the 3rd year:
A+2d=600(Equation 1)
2. For the 7th year:
A+6d=700(Equation 2)
Step 3: Solve the equations to find A and d.
Subtract Equation 1 from Equation 2:
(A+6d)−(A+2d)=700−600
This simplifies to:
4d=100
Thus, we find:
d=25
Now substitute d back into Equation 1 to find A:
A+2(25)=600
A+50=600
A=600−50=550
Step 4: Answer the questions.
i. Production in the first year (A):
A=550 units
ii. Total production in 7 years:
The total production in the first 7 years can be calculated using the formula for the sum of the first n terms of an AP:
Sn=n2⋅(2A+(n−1)d)
For n=7:
S7=72⋅(2⋅550+6⋅25)
Calculating this:
S7=72⋅(1100+150)=72⋅1250=87502=4375
iii. Production in the 10th year (A10):
Using the nth term formula:
A10=A+9d
Substituting the values:
A10=550+9⋅25=550+225=775
Final Answers:
i. Production in the first year = 550 units
ii. Total production in 7 years = 4375 units
iii. Production in the 10th year = 775 units
- Production in the 3rd year (A3) = 600 units
- Production in the 7th year (A7) = 700 units
- The production increases uniformly by a fixed number (d) each year.
The nth term of an AP can be expressed as:
An=A+(n−1)⋅d
where:
- A = first term (production in the first year)
- d = common difference (increase in production each year)
Using the formula for the nth term, we can write:
1. For the 3rd year:
A+2d=600(Equation 1)
2. For the 7th year:
A+6d=700(Equation 2)
Subtract Equation 1 from Equation 2:
(A+6d)−(A+2d)=700−600
This simplifies to:
4d=100
Thus, we find:
d=25
A+2(25)=600
A+50=600
A=600−50=550
i. Production in the first year (A):
A=550 units
The total production in the first 7 years can be calculated using the formula for the sum of the first n terms of an AP:
Sn=n2⋅(2A+(n−1)d)
For n=7:
S7=72⋅(2⋅550+6⋅25)
Calculating this:
S7=72⋅(1100+150)=72⋅1250=87502=4375
Using the nth term formula:
A10=A+9d
Substituting the values:
A10=550+9⋅25=550+225=775
i. Production in the first year = 550 units
ii. Total production in 7 years = 4375 units
iii. Production in the 10th year = 775 units
Topper's Solved these Questions
Similar Questions
A manufacturer of radio sets produced 600 units in the third year and 700 units in the seventh year. Assuming that the product increases uniformly by a fixed number every year, find i. the production in the first year ii. the total product in 7 years and iii. the product in the 10th year.
View SolutionA manufacture of TV set produced 600 sets in the third year and 700 sets in the seventh year. Assuming that the production increases uniformly by a fixed number every year, find:
(i) the production in the first year
(ii) the production in the 10th year.
(iii) the total production in first 7 years.
View Solution
Knowledge Check
In which year was the total production of scooters the maximum?
A1989B1986C1987D1995The table shows the production of different types of cars (in thousands).
यह तालिका अलग-अलग प्रकार के कारों का उत्पादन ( हज़ार में) दर्शाती है |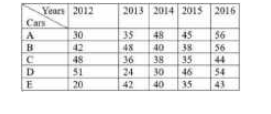 The number of years, in which the production of cars of type B is less than the average production of type D cars over the years is:
The number of years, in which the production of cars of type B is less than the average production of type D cars over the years is:
कितने वर्ष B प्रकार की कारों का उत्पादन इन वर्षों के दौरान D प्रकार की कारों के औसत उत्पादन से कम रहा है ?A4B1C3D2
A manufacturer of TV sets produced 600 sets in the third year and 700 sets in the seventh year. Assuming that the production increases uniformly by a fixed number every year, find :(i) the production in the 1st year(ii) the production in the 10th year(iii) the total production in first 7 years
View SolutionA manufacturer of T.V. serts produced 600 units in the third year and 700 units in the seventh year. Assuming the production uniformly increases by a fixed number every year, find:
(i) the production in the first year
(ii) The production in the 10 year and
(iii) the total prodction in 7 years.
View SolutionA manufacturre of TV sets produced 6000 units in the third year and 7000 units in the seventh year. Assuming that the production increases uniformaly by fixed number every year, find the production increases uniformly, by a fixed number every year, find the production (i) in the first year, (ii) in the 10th year, (iii) in 7 years.
View SolutionA manufacturer of wire produced 1400 m wire in the 5 th year and 1600 m in the 9th year. Assuming that the production increases uniformly by a fixed number every year, find
(i) the production in the 12th year.
(ii) in which year the production will be 1900 m?
(iii) the total production in 9 years.
View SolutionThe production of TV in a factory increases uniformly by a fixed number every year .It produced 8000 TV's in 6th year & 11300 in 9th year , find the production in 8th year .
View SolutionThe production of TV sets in a factory increases uniformly by a fixed number every year. It produced 16000 sets in 6th year and 22600 in 9th year. Find the production during (i) first year (ii) 8th year (iii) first 6 years.
View Solution
