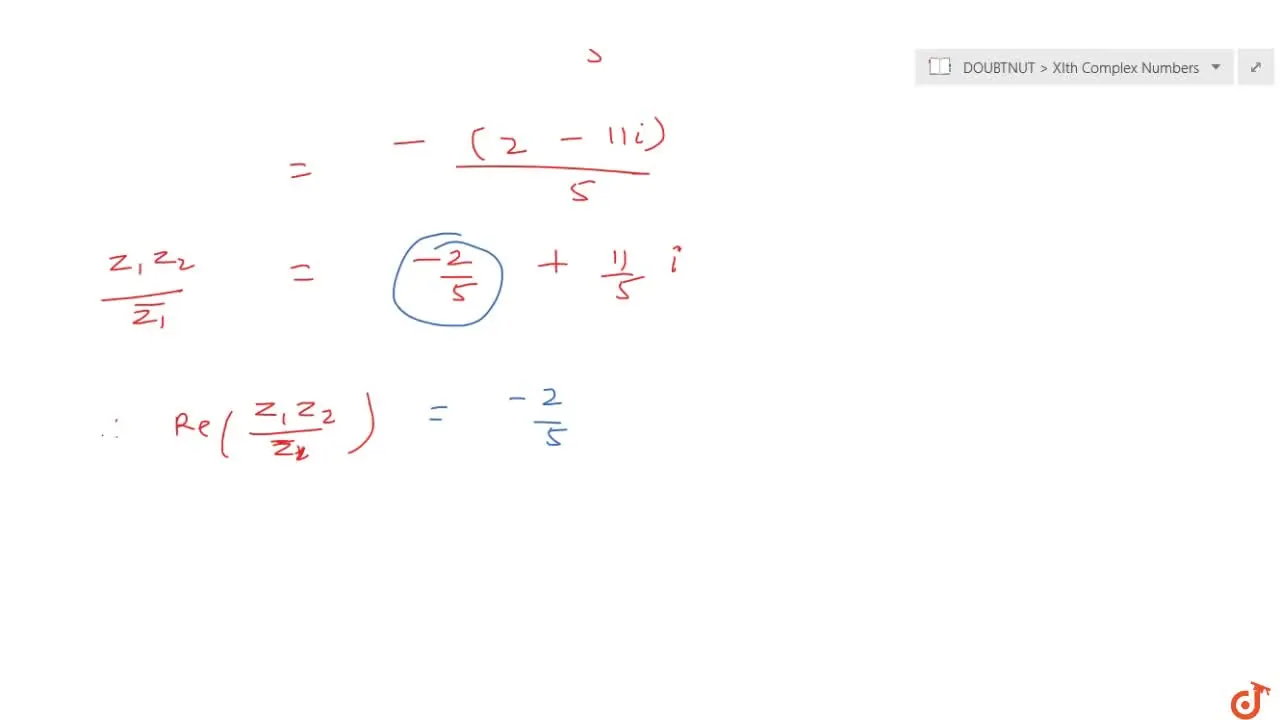If z1=2−i, z2=−2+i, find : Re(z1z2¯¯¯z1)
Video Solution
Text Solution
We have given: z1=2−i, z2=−2+i
then we have to find Re(z1z2¯¯¯z1)
Take,
z1z2=(2−i)(−2+i)=−4+2i+2i−(i2)
=−4+4i−(−1)=−3+4i......{since (i2)=−1}
As z1=2−ithen ¯¯¯z1=2+i
So, (z1z2¯¯¯z1)=−3+4i2+i
Now multiply and divide R.H.S by (2−i) we get
(z1z2¯¯¯z1)=(−3+4i)(2−i)(2+i)(2−i)
(z1z2¯¯¯z1)=−3(2−i)+4i(2−i)(22)−(i2)
(z1z2¯¯¯z1)=−6+3i+8i−4(i2)4−(i2)
(z1z2¯¯¯z1)=−2+11i5
Hence the real part of it is Re(z1z2¯¯¯z1)=(−25)
|
Updated on:21/07/2023
Related Playlists
Similar Questions
If z1=2−i, z2=−2+i, find : Re(z1z2¯¯¯z1)
View SolutionLet z1=2−i,z2=−2+i find (a) Re(z1z2z1)
View SolutionLet z1=2−i,z2=−2+i. Find
Re (z1z2¯z'1)View SolutionIf z1=2−i, z2=1+i, find ∣∣∣z1+z2+1z1−z2+i∣∣∣.
View SolutionIf z1=2−i, z2=−2+i, find : Im(1z1¯¯¯z1).
View SolutionIf z1=2−i,z2=1+i,find ∣∣∣z1+z2+1z1−z2+i∣∣∣
View Solutionif z1=3−iandz2=−3+i, then find Re(z1z2¯z1)
View Solutionif z1=1−iandz2=−2+4i then find Im(z1z2¯z1)
View SolutionIf z1=2−i and z2=−2+i, then Re(1z1¯¯¯z2)= . . . .
View Solutionif z1andz2 are 1−i,−2+4i respectively find Im(z1z2¯z1)
View Solution