If A={x∈C:x2=1} and B={x∈C:x4=1} , then write A−B and B−A.
Given 1A={x∈c:x2=1}
={x∈c:x=±1}
={1,−1}
soA={1,−1}
similarly we get B={1,−1,i,−i}
A−B={1,−1}−{1,−1,i,−i}<br>={ϕ}
B−A={1,−1,i,−i}−{1,−1}
={i,−i}
Topper's Solved these Questions
Similar Questions
If A={x∈C:x2=1} and B={x∈C:x4=1} , then write A−B and B−A.
View SolutionIf a and b denote the sum of the coefficients in the expansions of (1−3x+10x2)nand (1+x2)n respectively, then write the relation between a and b.
View SolutionIf A={x:x≤5,x∈N},B={x:x≤10,x∈N}andC={x:2<x<6,x∈N} then prove that A−(B∩C)={1,2}
View SolutionIf the lines x+ay+a=0, bx+y+b=0 and cx+cy+1=0 are concurrent, then write the value of 2abc−ab−bc−ca.
View SolutionIf f(x)={x, x≤1x2+bx+c, x>1 , then find the values of b and c if f(x) differentiability at x=1.
View SolutionIf A={2x:x∈Nand1≤x<4},B={(x+2):x∈Nand2≤x<5} } and C={x:x∈Nand4<x<8}, find : (i) A∩B (ii)A∪B (iii) (A∪B)∩C
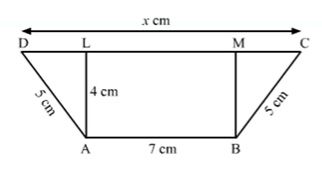
View SolutionIn Figure, ABCD is a trapezium in which AB=7cm, AD=BC=5cm, DC=x cm, and distance between AB and DC is 4cm . Find the value of x and area of trapezium ABCD
View SolutionLet f, g and h be real-valued functions defined on the interval [0, 1] by f(x)=ex^2+e−x^2, g(x)=xex^2+e−x^2 and h(x)=x2ex^2+e−x^2 . If a,b, and c denote respectively, the absolute maximum of f, g and h on [0, 1], then a=b and c≠b (b) a=c and a≠b a≠b and c≠b (d) a=b=c
View SolutionThe equations of the sides AB, BC and CA oftriangleA B C are y−x=2, x+2y=1 and 3x+y+5=0 respectively. The equation of the altitude through B is x−3y+1=0 b. x−3y+4=0 c. 3x−y+2=0 d. none of these
View SolutionIf the mean of observations x1, x2, .., xn is x , then the mean of x1+a, x2+a, , xn+a is (a) ax (b) x−a (c) x+a (d) xa
View Solution

