Let A={a,b,{c,d}, e}
. Which of the following statements are false and why?
(i){c,d}⊂A
(ii){c,d}∈A
(iii){{c,d}}⊂A
i) False
{c,d} is not a subset of A but it belongs to A.
Hence, {c,d}∈A
ii)True
Thus, {c,d}∈A
iii) True
Since, {c,d} is a subset of A.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Suppose a,b,c,d ∈C and let A =[abcd] . Then which one of the following is not true ?
A|det(A)|≤+|a|+|b|+|c|+|d|B|det(A)|≤(|a|+|b|)(|c|+|d|)C|det(A)|≤(|a|+|c|)(|b|+|d|)D|det(A)|≤√|a|2+|b|2√|c|2+|d|2
Let A={a,b,{c,d}, e} . Which of the following statements are false and why?
(i){a,b,e}i⊂A
(ii){a,b,c}⊂A
(iii){ϕ}⊂A
View SolutionLet A= {1,2,{3,4},5}. Which of the following statements are correct and why ?
(i) {3,4}⊂A
(ii) {3,4}∈A
(iii) {{3,4}}⊂A
(iv) 1∈A
(v)1⊂A
(vi) {1,2}⊂A.
(vii) {1,2,5}∈A
(viii) {1,2,3}⊂A.
(ix) ϕ∈A
(x) ϕ⊂A
(xi) {ϕ}⊂A.
View SolutionLet A={ϕ,{ϕ},2,{2,ϕ},3}, which of the following are true ? (i)ϕ∈A(i)ϕ⊂A(iii){ϕ}∈A(iv){ϕ}⊂A(v)2⊂A(vi){2,ϕ}⊂A(vii){{2},{3}}⊂A(viii){2,3}∉A(ix){ϕ,2,3}⊂A.
View SolutionIf sinθ=12 then θ=
View SolutionLet A={a,b,c,d},B={b,c,d,e}. Then n[(A xx B)nn(Bxx A ) equals to
View SolutionIn Figure, which of the following statements must be true? (i) a+b=d+c (ii) a+c+e=1800 (iii) b+f=c+e (a) (i) only (b) (ii) only (c) (iii) only (d) (ii) and (iii) only
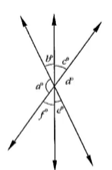
View SolutionLet A={a,b,c,d},B={c,d,e} and C={d,e,f,g}. Then verify each of the following identities:
(i) A×(B∩C)=(A×B)∩(A×C)
(ii) A×(B−C)=(A×B)−(A×C)
(iii) (A×B)∩(B×A)=(A∩B)×(A∩B)
View Solution

