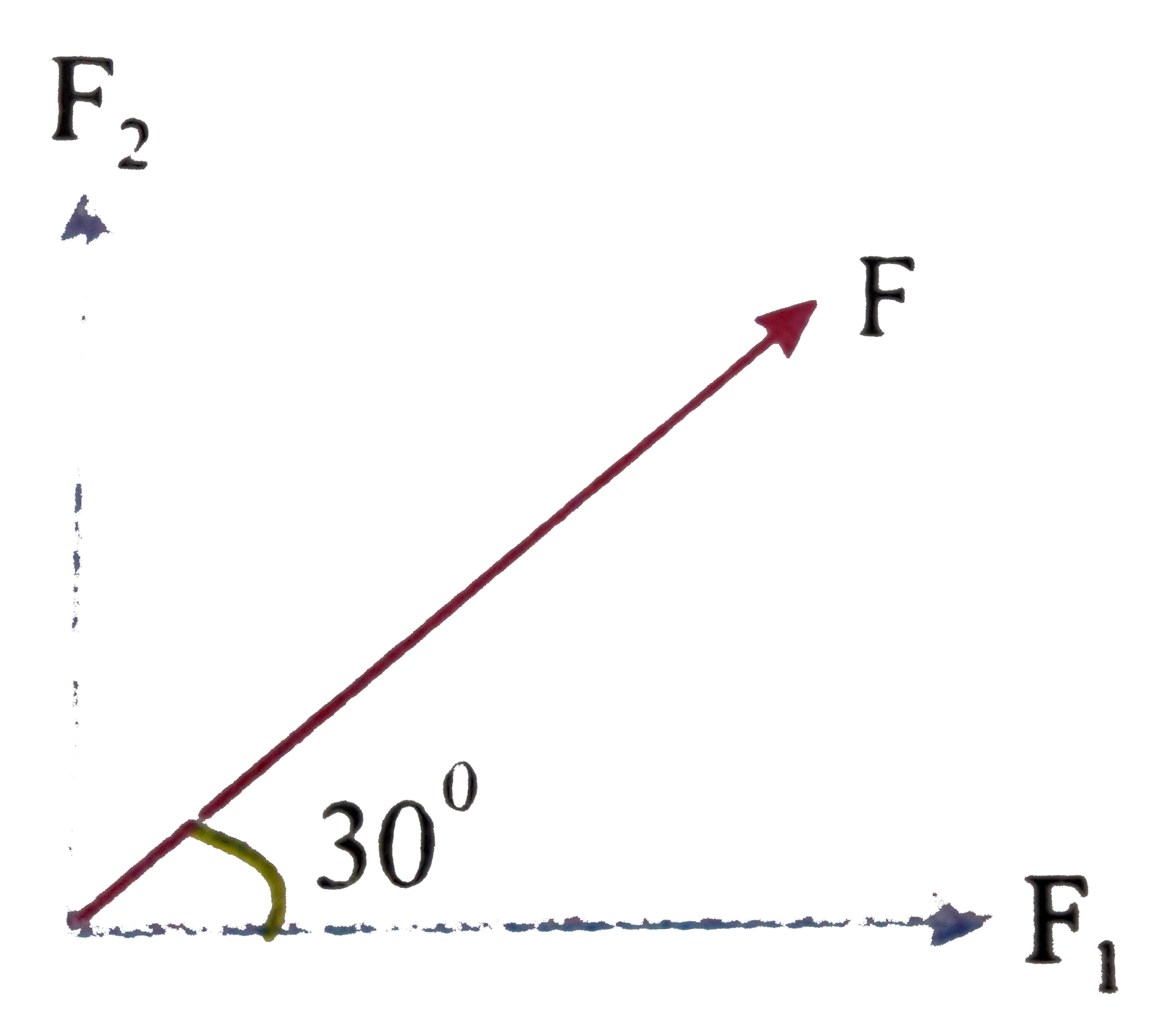
A force of 10N is resolved into the perpendiuclar components. If the first component makes $30^{\circ}$ with the force, the magnitudes of the components are

A

5N, 5N

B

$5 \sqrt{2} N, 5 N$

C

$5 \sqrt{3} N, 5 N$

D

$10 N, 10 \sqrt{3} N$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

|

Updated on:21/07/2023

Class 11 PHYSICS VECTOR

Topper's Solved these Questions

Similar Questions

One of the two rectangular components of a force is 25N and it makes an angle of $60^{0}$ with the force.The magnitude of the other component is
View Solution
One of the rectangular components of a force of $50 N$ is $25 N$ . The magnitude of other component is.
View Solution

Knowledge Check

Question 1 - Select One
One of the two rectangular components of a force is $20 N$ and it makes an angle of $30^{\circ}$ with the force. The magnitude of the other component is
A $10 / \sqrt{3}$
B $20 / \sqrt{3}$
C $15 / \sqrt{3}$
D $40 / \sqrt{3}$
Question 2 - Select One
One of the two rectangular components of a force is 10 N and it makes an angle 60° with the force. The magnitude of the force is :
A7.1 N
B14.1 N
C17.3 N
D20 N
Question 3 - Select One
Consider the following statements
The work done by the force is defined to be the product of component of the force in the direction of the displacement and the magnitude of this displacement.
Wok done $W = (F cos Θ)$ , d=F.d which of the following option is correct ?
AOnly I
BOnly II
CI and II
Dnone of these

NARAYNA-VECTORS-LEVEL-I (C.W)

Home
Ask Doubt
Profile