On face of a glass (μ=1.50) lens is coated with a thin film of magnesium fluoride MgF2(μ=1.38) to reduce reflection from the lens surface. Assuming the incident light to be perpendicular to the lens surface. The least coating thickness that eliminates the reflection at the centre of the visible spectrum (λ=550nm) is about
0.05μm
0.10μm
1.38μm
2.80μm
The correct Answer is:B
To find the least coating thickness of magnesium fluoride (MgF₂) that eliminates reflection at the center of the visible spectrum (λ = 550 nm), we can use the principle of destructive interference for thin films.
1. Understanding the Condition for Destructive Interference:
For a thin film, destructive interference occurs when the path difference between the light reflected from the top and bottom surfaces of the film leads to a phase difference of an odd multiple of π (or λ/2). The condition for destructive interference is given by:
2nT=(m+12)λ
where:
- n is the refractive index of the film (MgF₂ in this case),
- T is the thickness of the film,
- m is an integer (0, 1, 2, ...),
- λ is the wavelength of light in vacuum.
2. Using the First Order of Destructive Interference:
For the least thickness that eliminates reflection, we can take m=0:
2nT=12λ
Rearranging gives:
T=λ4n
3. Substituting the Values:
Given:
- λ=550nm=550×10−9m
- n=1.38 (for MgF₂)
Substituting these values into the equation:
T=550×10−94×1.38
4. Calculating the Thickness:
First, calculate 4×1.38:
4×1.38=5.52
Now substitute this back into the equation for T:
T=550×10−95.52≈99.64×10−9m
Converting this to micrometers:
T≈0.1μm
5. Final Answer:
The least coating thickness that eliminates reflection at the center of the visible spectrum is approximately:
T≈0.1μm
For a thin film, destructive interference occurs when the path difference between the light reflected from the top and bottom surfaces of the film leads to a phase difference of an odd multiple of π (or λ/2). The condition for destructive interference is given by:
2nT=(m+12)λ
where:
- n is the refractive index of the film (MgF₂ in this case),
- T is the thickness of the film,
- m is an integer (0, 1, 2, ...),
- λ is the wavelength of light in vacuum.
For the least thickness that eliminates reflection, we can take m=0:
2nT=12λ
Rearranging gives:
T=λ4n
Given:
- λ=550nm=550×10−9m
- n=1.38 (for MgF₂)
T=550×10−94×1.38
First, calculate 4×1.38:
4×1.38=5.52
Now substitute this back into the equation for T:
T=550×10−95.52≈99.64×10−9m
Converting this to micrometers:
T≈0.1μm
The least coating thickness that eliminates reflection at the center of the visible spectrum is approximately:
T≈0.1μm
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.57
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.58
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.55
Explore 9 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 21 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCEChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
A glass lens is coated on one side with a thin film of magnesium fluoride (MgF2)to reduce reflection from the lens surface (Fig. 2.26). The Index of refraction of MgF2 is 1.38, that of the glass is 1.50. What is the least coating thickness that eliminates (via interference) the reflections at the middle of the visible specturm (λ=550nm)? Assume that the light is approxmately perpendicular to the lens surface.
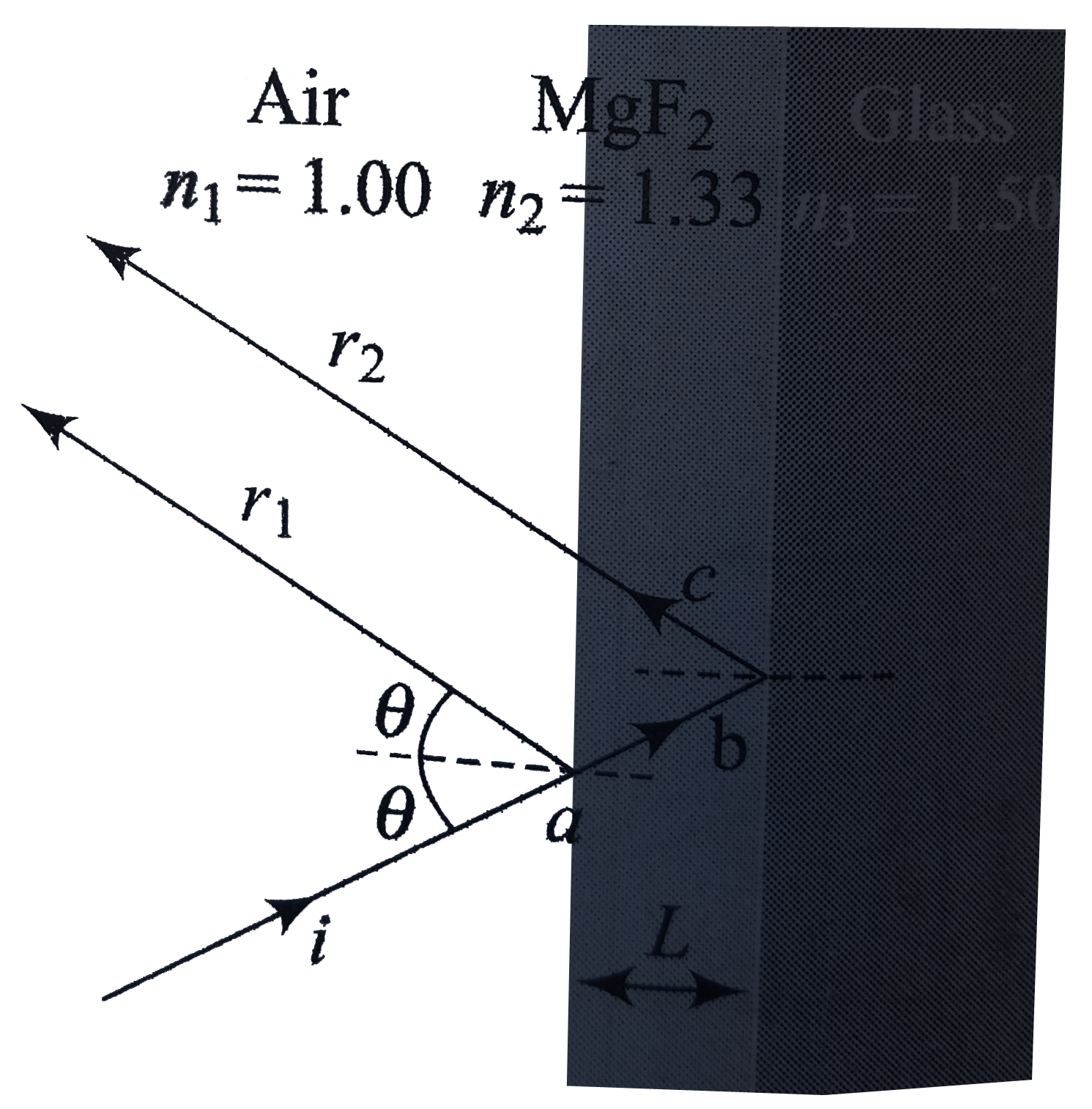
View SolutionIn solar cells, a silicon solar cell (μ=3.5) is coated with a thin film
of silicon monoxide SiO(μ=1.45) to minimize reflective losses from the surface.
Determine the minimum thickness of SiO that produces the least reflection at a
wavelength of 550nm, near the centre of the visible spectrum. Assume
approximately normal incidence .
View Solution
Knowledge Check
To ensure almost 100% transmittivity, photographic lenses are often coated with a thin layer of dielectric maerial, like MgF2(μ=1.38) . The minimum thickness of the film to be used so that at the centre of visible spectrum (λ=5500Å) there is maximum transmission.
A1000ÅB2000ÅC4000ÅD500ÅA double convex thin lens made of glass (refractive index μ=1.5) has both radii of curvature of magnitude 20 cm . Incident light rays parallel to the axis of the lens will converge at a distance L such that
AL=20 cmBL=10 cmCL=40 cmDL=20/3 cmA double convex thin lens made of glass (refractive index μ=1.5) has both radii of curvature of magnitude 20 cm . Incident light rays parallel to the axis of the lens will converge at a distance L such that
AL=20cmBL=10cmCL=40cmDL=20/3cm
A lens (μ=1.5) is coated with a thin film of refractive index 1.2 order to reduce the reflected form its surface atλ=4800Å.Find the maximum thickness of the film which will minimized the intensity of the reflected light .(Assume near normal incidence)
View SolutionA thin film of thickness 4×10−5 cm and μ=1.5 is iluminated by white light incident normal to its surface. What wavelength in the visible range be intensified in the reflected beam ?
View SolutionThe outer surface of a transparent glass slab of refractive index μS=1.5 is coated by a thin layer of transparent medium of refractive index μC=1.6. Orange light of wavelength 6400Å falls normally on the coating. The reflected light at the upper surface and at the lower surface of teh coat interfere destructively. If thickness of the coat is 5K×10−8m, calculate the minimum value of K.
View SolutionWhat is the thinnest film of coating with n= 1.42 on glass (n=1.52) for which destructive interference of the red component (650 nm) of an incident white light beam in air can take place by reflection ?
View SolutionA biconvex thick lens is constructed with glass (mu = 1.50). Each of the surfaces has a radius of 10 cm and the thickness at the middle is 5 cm. Locate the image of an object placed far away from the lens.
View Solution

