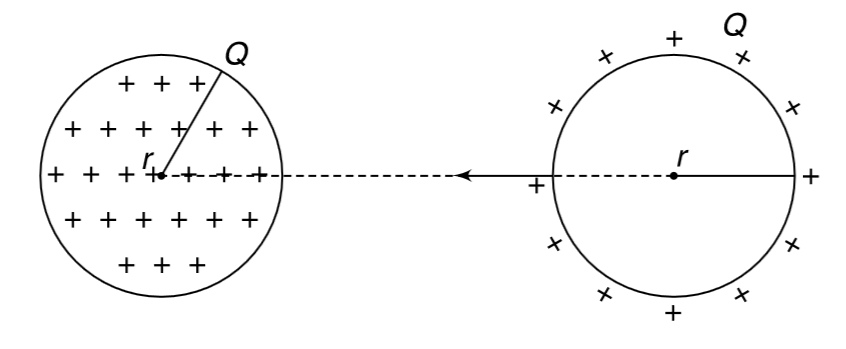
Consider a spherical shell of radius R wil a total charge +Q uniformly spread on its surface (centre of the shell lies at the origin x =0) Two point charge 1 and -q are brought, one after the other, from far away and placed at x=−1/2 and x=+a/2(a<R) respectively. Magnitude of the work done in this process is
(Q+q)2/4πε0a
zero
q2/4πε0a
Qq/4πε0a
The correct Answer is:C

W1=q(KQR)⇒W2=(KQR+kqa)(−q)
W−−kq2a
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.44
Explore 10 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.45
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.42
Explore 20 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 21 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCEChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
There is a hemispherical shell having charge Q uniformly distributed on its surface. Radius of the shell is R. Find electric potential and field at the centre (of the sphere).
View SolutionThere is a ball of radius r having uniformly distributed volume charge Q on it and there is a spherical shell of radius r having uniformly distributed surface charge Q on it. The two spheres are far apart. (a) A point charge q is moved slowly from the centre of the shell (through a small hole in it.) to the centre of the ball. Find work done by the external agent in the process. (b) The two spheres are brought closer so that their centers are separated by 4r. Now calculate the amount of work needed in slowly moving a point charge q from the centre of the shell to the centre of the ball. Assume that charge on one ball does not alter the charge distribution of the other. Does your answers in (a) and (b) differ? Why?
View Solution
Knowledge Check
Consider a spherical shell of radius R with a total charge +Q uniformly spread on its surface (center of the shell lies at the origin x= 0). Two point charge, +q and −q are brought, one after the other, from far away and placed at x=−a/2 and x=+a/2(a<R), respectively. Magnitude of the work done in this process is
A(Q+q)2/4πε0aBzeroCq2/4πε0aDQq/4πε0aA thin spherical conducting shell of radius R has a charge q. Another charge Q is placed at the centre of the shell. The electrostatic potential at a point P a distance R2 from the centre of the shell is
A(a) 2Q4πε0RB(b) 2Q4πε0R−2q4πε0RC(c) 2Q4πε0R+q4πε0RD(d) (q+Q)24πε0RConsider a thin spherical shell of radius R consisting of uniform surface charge density σ. The electric field at a point of distance x from its centre and outside the shell is
Ainversely proportional to σBdirectly proportional to x2Cdirectlr proportional to RDinversely proportional to x2
A spherical shell of radius R1 with uniform charge q is expanded to a radius R2. Find the work performed by the electric forces in this process.
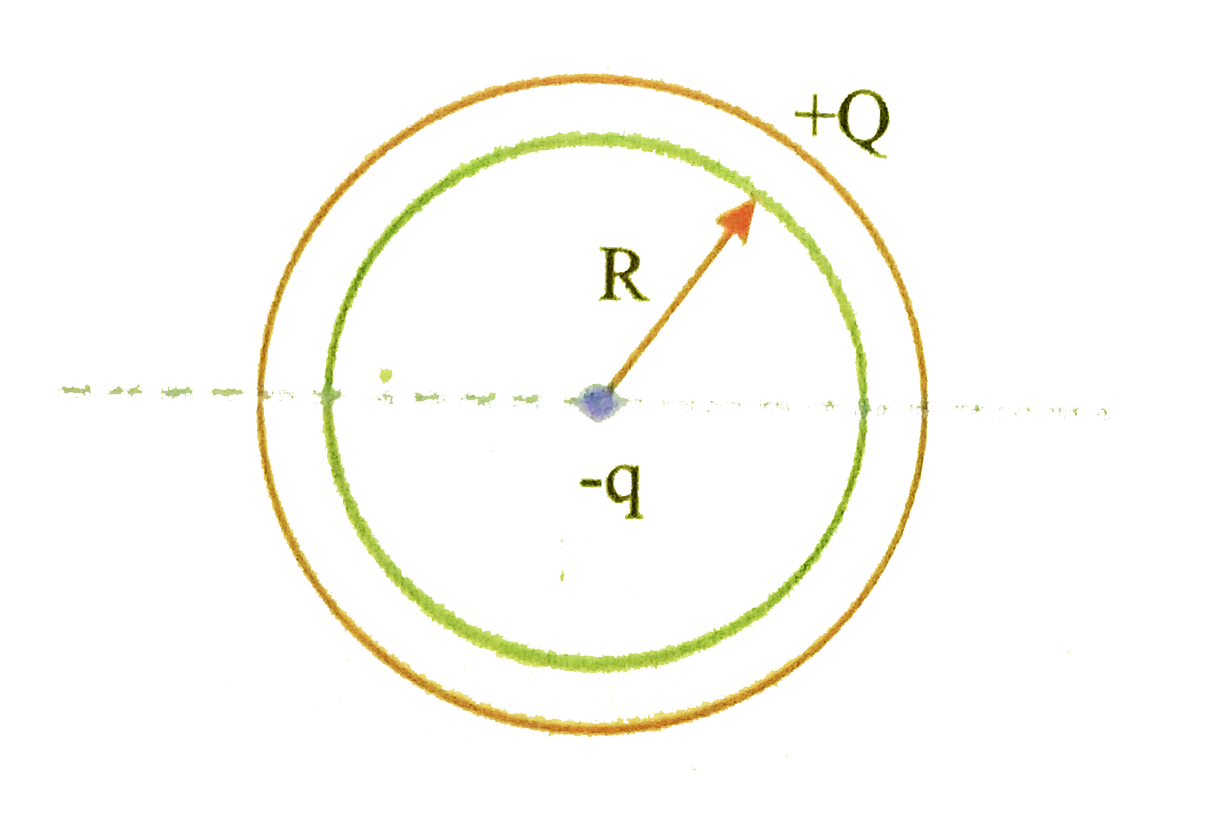
View SolutionA thin spherical shell radius of R has of charge Q unfromily distributed on it.At the centre of the shell ,a negative point charge −q is placed.IF the shell is cut into two identical hemisphere still equlibrium is maintained .Then find the relation between Q and q?
View SolutionA spherical conducting shell of inner radius r1 and outer radius r2 has a charge Q.
(a) A charge q is placed at the centre of the shell. What is the surface charge density on the inner and outer surfaces of the shell ?
View SolutionA thin spherical conducting shell of radius R has a charge q. Another charge Q is placed at the centre of the shell. The electrostatic potential at a point P a distance R2 from the centre of the shell is
View SolutionA spherical shell of radius R is given charge 3q on its surface and a point charge q is placed at distance R/2 from its centre C. Also there is a charge 2q placed outside the shell at a distance of 2R as shown. Then

View Solution

