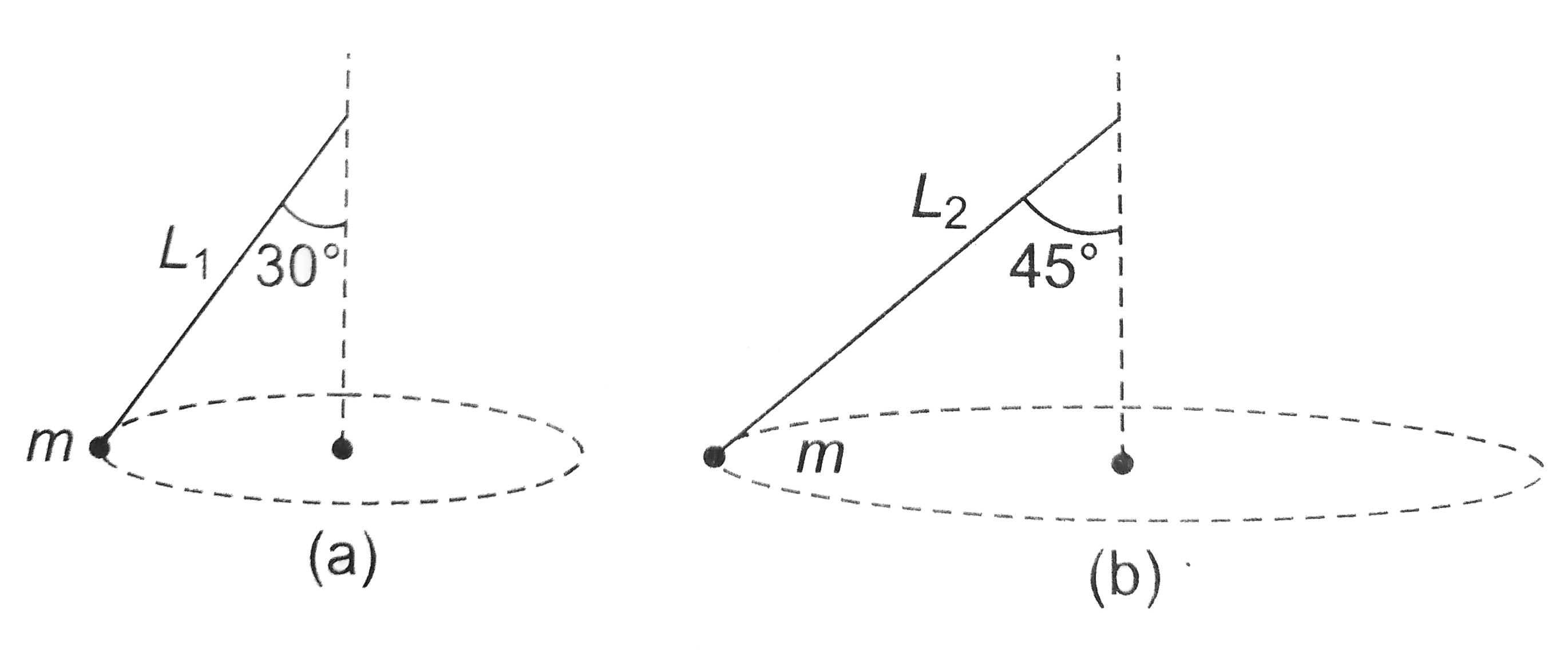
Two partical tied to different strings are whirled in a horizontal circle as shown in figure. The ratio of lengths of the string so that they complete their circular path with equal time priod is:
√32
√23
1
None of these
The correct Answer is:B
Since T=2π√Lcosθg
∴T1=T2
⇒L1cosθ1=L2cosθ2
∴L1L2=cosθ2cosθ1=cos45∘cos30∘
L1L2=√2√3.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.43
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.44
Explore 10 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.41
Explore 9 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 21 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCEChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
A stone of mass 0.2 kg is tied to one end of a string of length 80cm Holding the other end, the stone is wirled into a vertical circle. What is the minimum speed of the stone at the lowest point so that it just completes the circle What is the tension in the string at the lowest point of the circular path ? . (g=10−2) .
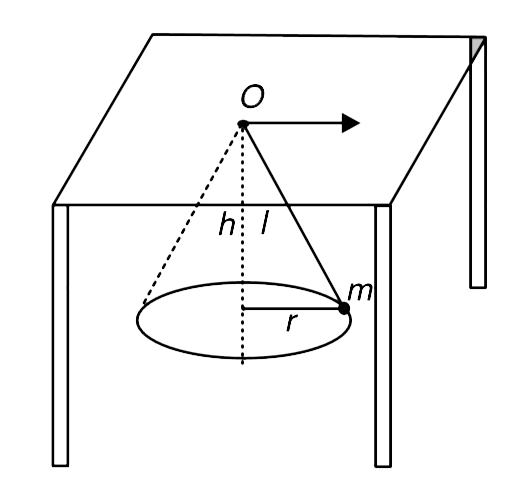
View SolutionA mass m in attached to a mass less string and swings in a horizontal circle, forming a conical pendulum, as shown in the figure. The other end of the string passes through a hole in the table and is dragged slowly so as to reduce the length l. The string is slowly drawn up so that the depth h shown in the figure becomes half. By what factor does the radius (r) of the circular path of the mass m change?
View Solution
Knowledge Check
A stone is tied to the end of a string of length 1 and whirled in a horizental circle. When the string breaks then stone
Aflies radially inwoardsBfiles radially outwardsCdrops downDflies tangent to the circular pathA particle mass is tied to an ideal string and whirled in a vertical circle of radius L, where L is off-course the length of the string. If the ratio of the maximum to minimum tension in the string throughout the motion is 2 : 1, then the maximum possible speed of the partcle will be:
A√11gLB√5gLC√10gLDsqrt(3 gL)A stone tied to a string of length l is whirled in a horizontal circle at a constant angular speed ω in a circle of radius r. If the string makes an angle θ with vertical then the tension in the string is :
Am(gcosθ+ω2r)Bm√ω4r2+g2Cm√ω2r2+g2Dm(gcosθ−ω2r)
A stone of mass m tied to the end of a string, is whirled around in a horizontal circle. (Neglect the force due to gravity). The length of the string is reduced gradually keeping the angular momentum of the stone about the centre of the circle constant. Then, the tension in the string is given by T=Ar2 where A is a constant, r is the instantaneous radius fo the circle and n=....
View SolutionA particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
View SolutionIF a stone is tied to one end of the string and whirled in verticle circle, then the tension in the string at the lowest point is equal to
View SolutionA small steel shphere tied at the end of a string is whirled in a horizontal circle with uniform angular velocity ω the string is suddently pulled so that the radius of the circle is halved .If ω2 is the angular velocity then
View SolutionA boy is whirling a stone tied with a string in a horizontal circular path. When the string breacks, the stone
View Solution

