A block of mass m starts at rest at height on a frictionless inclined plane. The block slides down the plane, travels across a rough horizontal surface with coefficient of kinetic friction μ and compresses a spring with force constant k a distance x before momentarilly coming to rest. Then the spring extends and the block travels back across the rough surface, sliding up the plane. The block travels a total distance d on rough horizontal surface. The correct experssion for the maximum height h' that the block reaches on its return is :

mgh'=mgh−μmgd
mgh'=mgh+μmgd
mhg'=mgh+μgd+kx2
mgh'=mgh−μmgd−kx2
The correct Answer is:A
Final P.E of block = Initial P.E of block + work done by friction
∴Mgh'=mgh−μmgd.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.22
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.23
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.20
Explore 9 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 21 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCEChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
A particle is projected at an angle 60∘ with speed 10(√3)m/s, from the point A, as shown in the figure. At the same time the wedge is made to move with speed 10(√3)m/s towards right as shown in the figure. Then the time after which particle will strike with wedge is
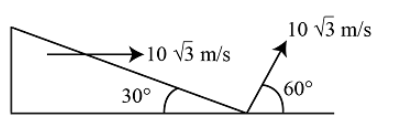
View SolutionA block B is pushed momentarily along a horizontal surface with an initial velocity v . If mu is the coefficient of sliding friction between B and the surface, block B will come to rest after a time:

View SolutionA metal is illumimated by light of two different wavelength 248nm and 310nm . The maximum speeds of the photoelectrons corresponding in these wavelength are u1andu2 respectively . If the ratio u1:u2=2:1 and hc=1240eVnm, the work function of the meal is nearly
View SolutionA galvanometer having 30 divisions has a current sensitivity of 20μA/division. It has a resistance of 25Ω. How will you convert it into an ammeter upto 1 ampere? How will you convert this ammeter into a voltmeter up to 1 volt?
View SolutionAn electromagnetic wave of frequency v=3.0MHz passes from vacuum into a dielectric medium with permittivity ε=4.0. Then
View SolutionA block slides down a rough inclined plane of slope angle θ with a constnat velocity. It is then projected up the same plane with an intial velocity v the distance travelled by the block up the plane coming to rest is .
View Solution(a) A block slides down an incline of angle 45^(@) with an acceleration (g)/(2 sqrt(2)) . Find the friction coefficient. (b) A block slides down at 45^(@) inclined plane in twice the time it takes to slide down a smooth 45^(@) incline. What is friction co-efficient between the block and the incline? ( c) A block slides down on a rough inclined plane of inclination 30^(@) with constant velocity. If this block is projected up the plane with a velocity of 10 m//s , then at what distance along the inclined plane , the block will come to rest? (d) A body is launched up on a rough inclined plane of inclination theta . If time of ascent is half of time of descent, find the friction coefficient.
View SolutionA block of mass m starts at rest at height on a frictionless inclined plane. The block slides down the plane, travels across a rough horizontal surface with coefficient of kinetic friction mu and compresses a spring with force constant k a distance x before momentarilly coming to rest. Then the spring extends and the block travels back across the rough surface, sliding up the plane. The block travels a total distance d on rough horizontal surface. The correct experssion for the maximum height h' that the block reaches on its return is :
View SolutionA block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is µ. At what angle of inclination theta of the plane to the horizontal will the block just start to slide down the plane?
View SolutionA block of mass m is at rest on a rough inclined plane, whose friction coefficient is μ. Net force exerted by surface on block is :-
View SolutionA block is at rest at the top of a rough inclined plane of inclination 30° with the horizontal. What is the coefficient of kinetic friction between the block and the plane, if the . block slides down with an acceleration of g5 ?
View SolutionA body freely released from A slides down a smooth inclined plane 'AB' and then a rough incline plane 'BC' such that BC = N (AB). If the block comes to rest at C, then coefficient of kinetic friction between the block and inclined plane is?
View SolutionA block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionA block slides down a rough inclined plane of slope angle theta with a constant velocity. It is then projected up the same plane with an initial velocity v. The distance travelled by the block up the plane before coming to rest is
View SolutionA cubical block rests on a plane rough surface with coefficient of static friction 1√3. AT what angle the plane be inclined so that the block just slides?
View SolutionA block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is µ. At what angle of inclination theta of the plane to the horizontal will the block just start to slide down the plane?
View Solution