A 1kg block B rests as shown on a bracket A of same mass. Constant forces F1=20N and F2=8N start to act at time t=0 when the distance of block B from pulley is 50cm. Time when block B reaches the pulley is …………………… .( Assume that friction is absent every where. Pulley and string are light.

The correct Answer is:0.5 sec
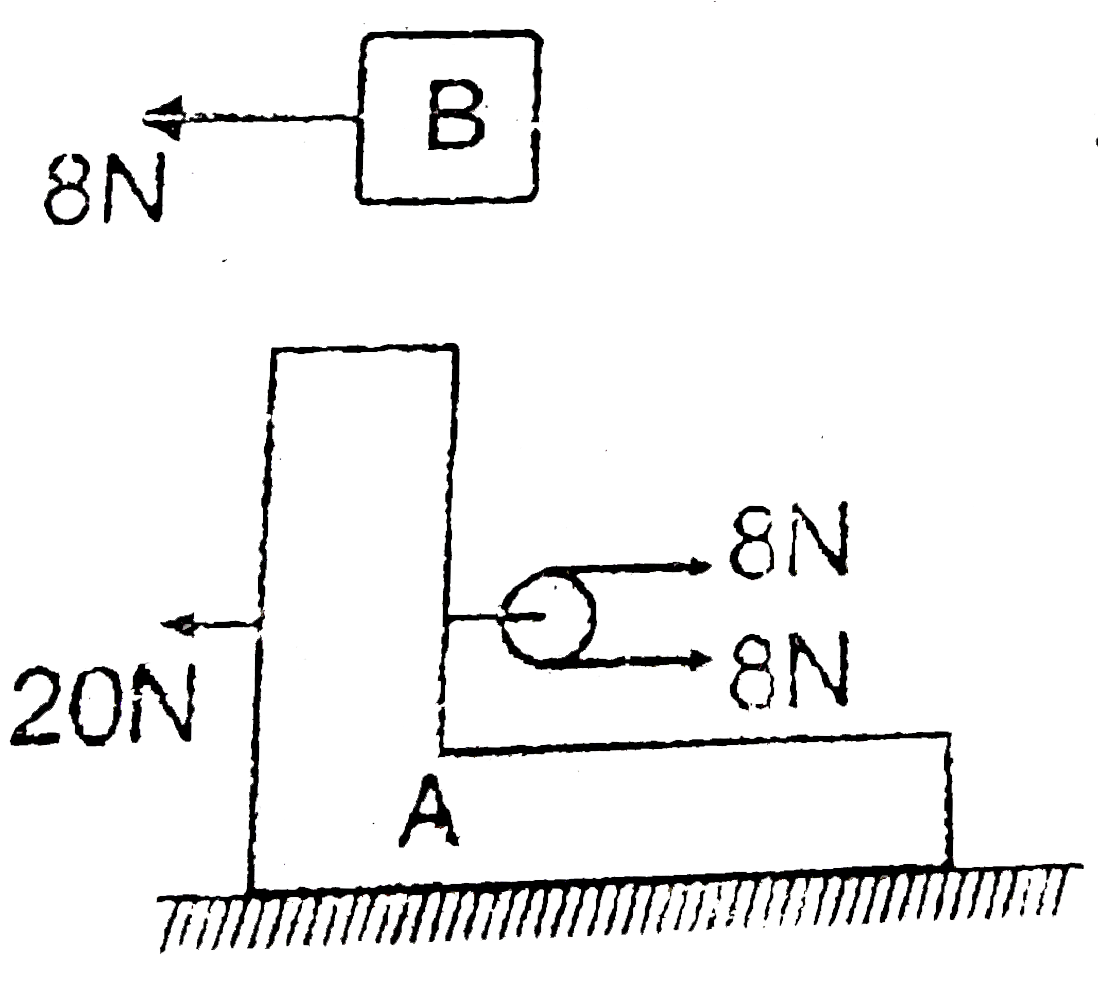
∴arel=8−4=4∴Srel=12arelt2
∴t=0.5sec.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.17
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.18
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.15
20 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
21 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
The velocities of A and B shown in fig. Find the speed (in ms−1) of block C. (Assume that the pulleys and string are ideal).

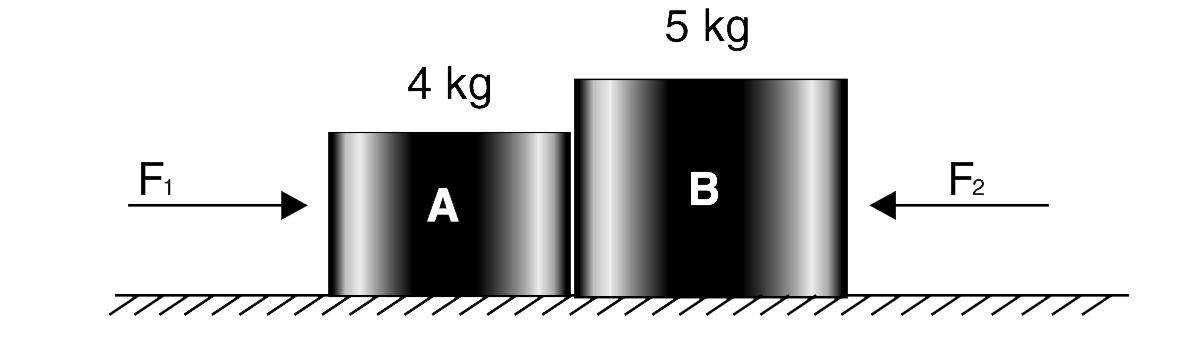
View SolutionTwo rectangular blocks A and B are placed on a horizontal surface at a very small separation. The masses of the blocks are mA=4 kg and mB=5 kg. Coefficient of friction between the horizontal surface and both the blocks is μ=0.4. Horizontal forces F1 and F2 are applied on the blocks as shown. Both the forces vary with time as F1=15+0.5t
F2=2t
Where ‘t’ is time in second.
Plot the variation of friction force acting on the two blocks (fAandfB) vs time till the motion starts. Take rightward direction to be positive for B and leftward direction to be positive forfA.
View Solution
Knowledge Check
In the system shown in figure mB=4kg , and mA=2kg . The pulleys are massless and friction is absent everywhere. The acceleration of block A is.
 A10/3m/s2B20/3m/s2C2m/s2D4m/s2
A10/3m/s2B20/3m/s2C2m/s2D4m/s2
A block B is placed over a cart which in turn lies over a smooth horizontal floor. Block A and Block C are connected to block B with light inextensible strings passing over light frictionless pulleys fixed to the cart as shown. Initially the blocks and the cart are at rest. All the three blocks have mass m and the cart has mass M(M=3m). Now a constant horizontal force of magnitude F is applied to block A towards right.
Q. Let the coefficient of friction between block B and cart is μ(μ>0) and friction is absent everywhere else. Then the maximum value of force F applied to block A such that there is no relative acceleration between block B and cart isAμmgB2μmgC3μmgD4μmgIn the figure shown, all surfaces are smooth and the pulley is massless. A constant force of magnitude F=mg2 is acting on the block of mass M. The acceleration of the block M is :
 Amg2(m+M) towards rightBmg2(m−M) towards rightsCmg2(m−M) towards leftDmg2(m+m) toward left
Amg2(m+M) towards rightBmg2(m−M) towards rightsCmg2(m−M) towards leftDmg2(m+m) toward left
Two blocks of mass 10 kg and 2 kg are connected by an ideal spring of spring constant K=800N/m and the system is placed on a horizontal surface as shown.
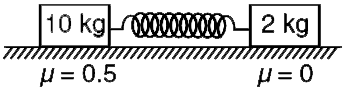
The coefficient of friction between 10 kg block and surface is 0.5 but friction is absent between 2 kg and the surface. Initially blocks are at rest and spring is relaxed. The 2 kg block is displaced to elongate the spring by 1 cm and is then released. (a) Will 10 kg block move subsequently? (b) Draw a graph representing variation of magnitude of frictional force on 10 kg block with time. Time t is measured from that instant when 2 kg block is released to move.
View SolutionBlocks m1 and m2 starts from rest and move to right with accelerations as shown. If t is in second then the time when block m3 again come to rest from t=0 is (pulley and strings are ideal) :
 .
.
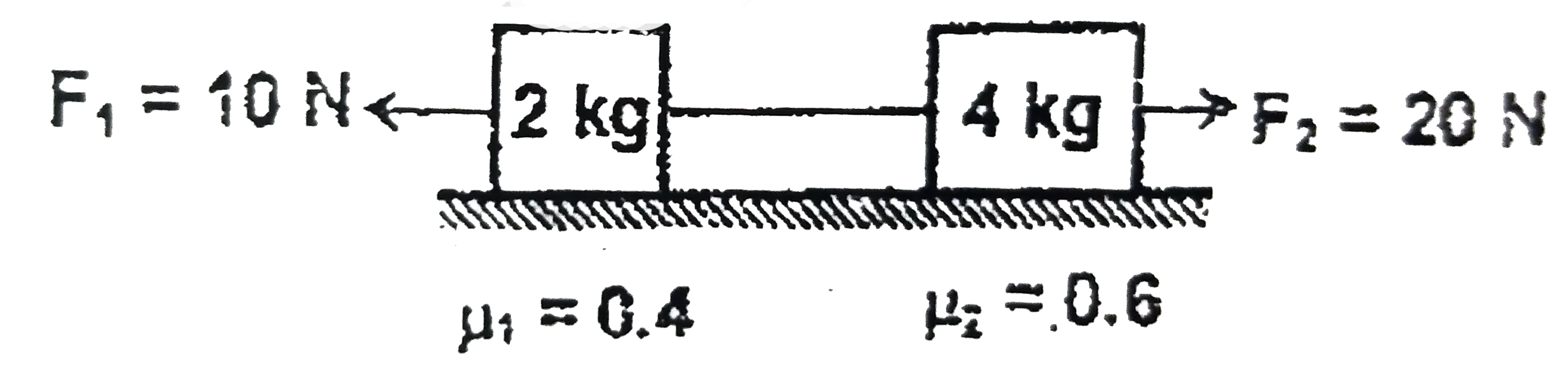
View SolutionTwo blocks of masses 2 kg and 4kg are connected through a massless inextensible string. The co-efficient of fricition between 2kg block and ground is 0.4 and the coefficient of friction between 4kg block and ground is 0.6. The forces F1=10N and F2=20N are applied on the blocks as shown in the figure. Calculate the frictional force between 4 kg block and ground (Assume initially the tension in the string was just before forces F1 and F2 wer applied).
View SolutionFor the given figure the acceleration of 1 kg block if string is massless and mass of pulley is 2 kg and diameter of pulley is 0.2 m :-
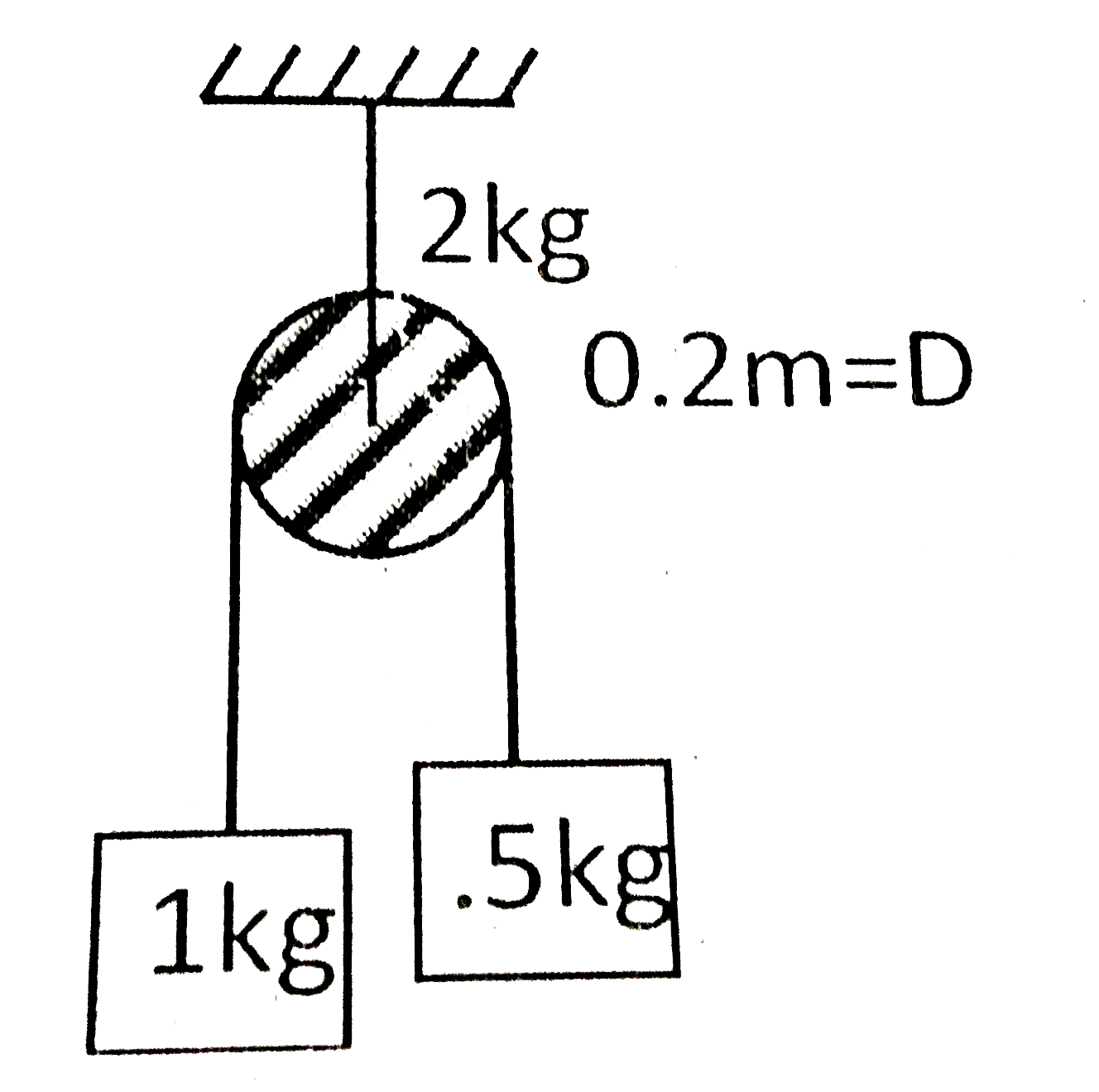
View SolutionThere blocks a,b and c of massses 10 kg ,10 kg and 20 kg respectivaly are arrenged as shown in figure all the surface are frictionless and string is inextensible A constant force F= 20N MN is applied on block a as shown .pulley and string are light . part of block a as shown . pulley and string are light . part of the string connecting both pulleys is vertical and part of hte stings connecting pulleys with masses a and b are horizontal .
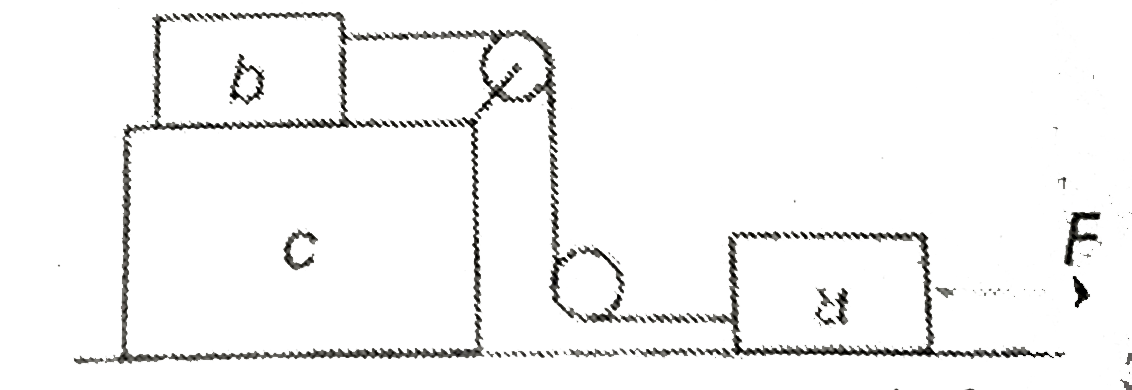
View Solution
