Find out the elongation in block. If mass area of cross-section and young modulus of block are m, A and y respectively.

Video Solution

Text Solution

Verified by Experts

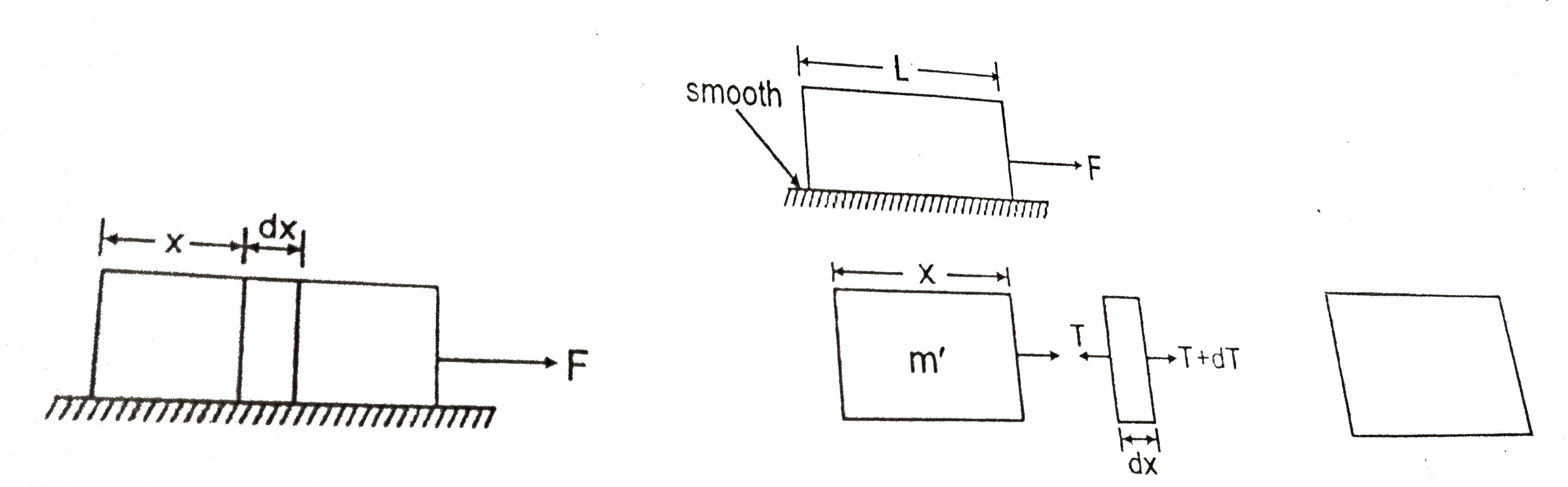
Acceleration, $a = \frac{F}{m}$ then $T = m' a$ where $\Rightarrow m' = \frac{m}{l} x$
$T = \frac{m}{l} \times \frac{F}{m} = \frac{F x}{l}$
Elongation in element $' d x' = \frac{T d x}{A y}$
totoal elongation , $δ = l \int 0 \frac{T d x}{A y} d = l \int 0 \frac{F x d x}{A l y} = \frac{F l}{2 A y}$

|

Updated on:21/07/2023

Class 11 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Each of three blocks shows in figure has a mass 3 kg. The wire connecting blocks A and B has area of cross-section $0.005 c m^{2}$ and Young's modulus of elasticity $Y = 2 \times 10^{11} N / m^{2}$ . Neglect friction. Find the elasticity potential energy stored per unit volume in wire connecting blocks A and B in steady state.
$(T a k e n g = 10 m / s^{2})$

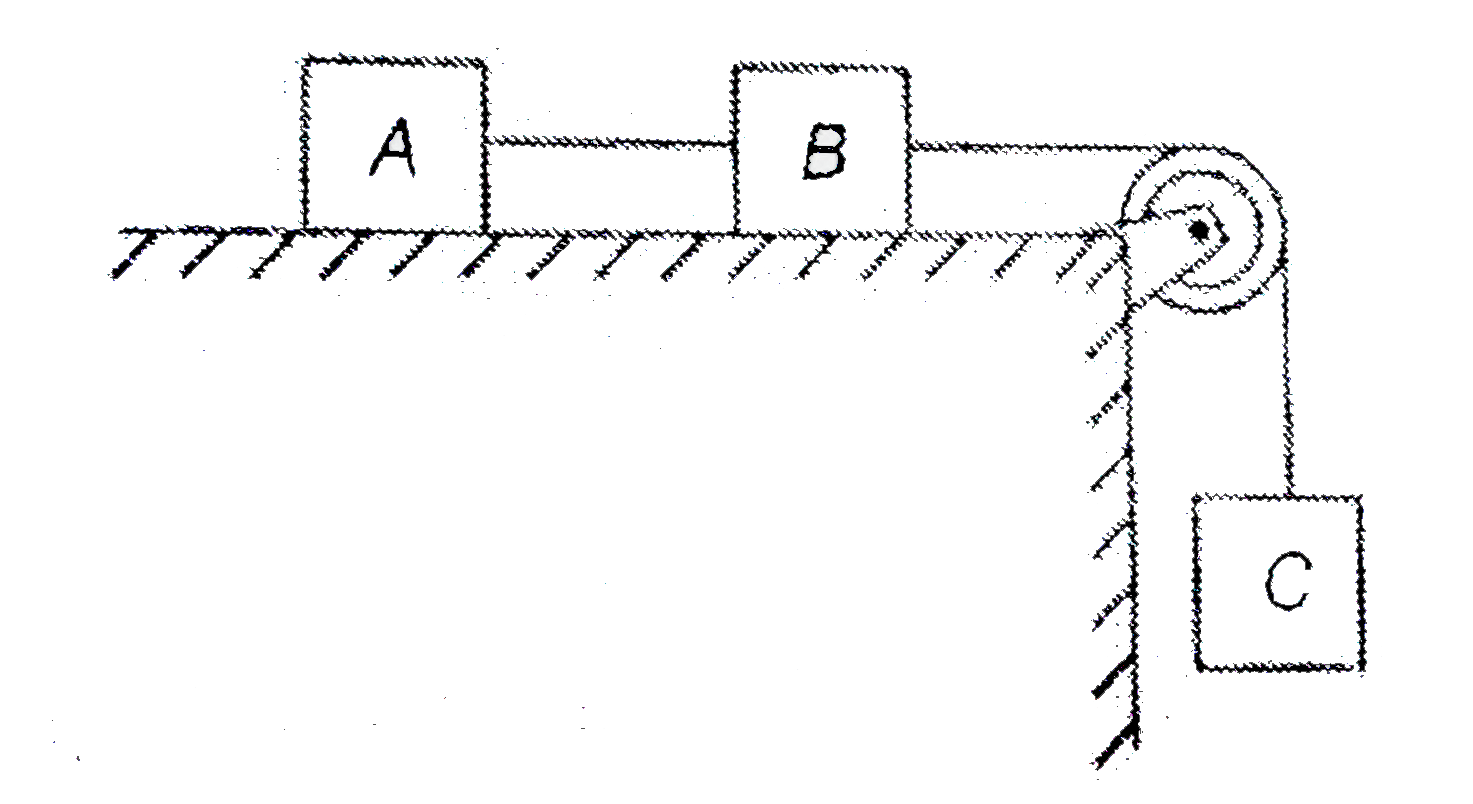A $500 J / m^{3}$
B $1000 J / m^{3}$
C $2000 J / m^{3}$
D $3000 J / m^{3}$
Question 2 - Select One
A metal wire of length L, area of cross-section A and Young's modulus Y behaves as a spring of spring constant k.
A $k = Y A / L$
B $k = 2 Y A / L$
C $k = Y A / 2 L$
D $k = Y L / A$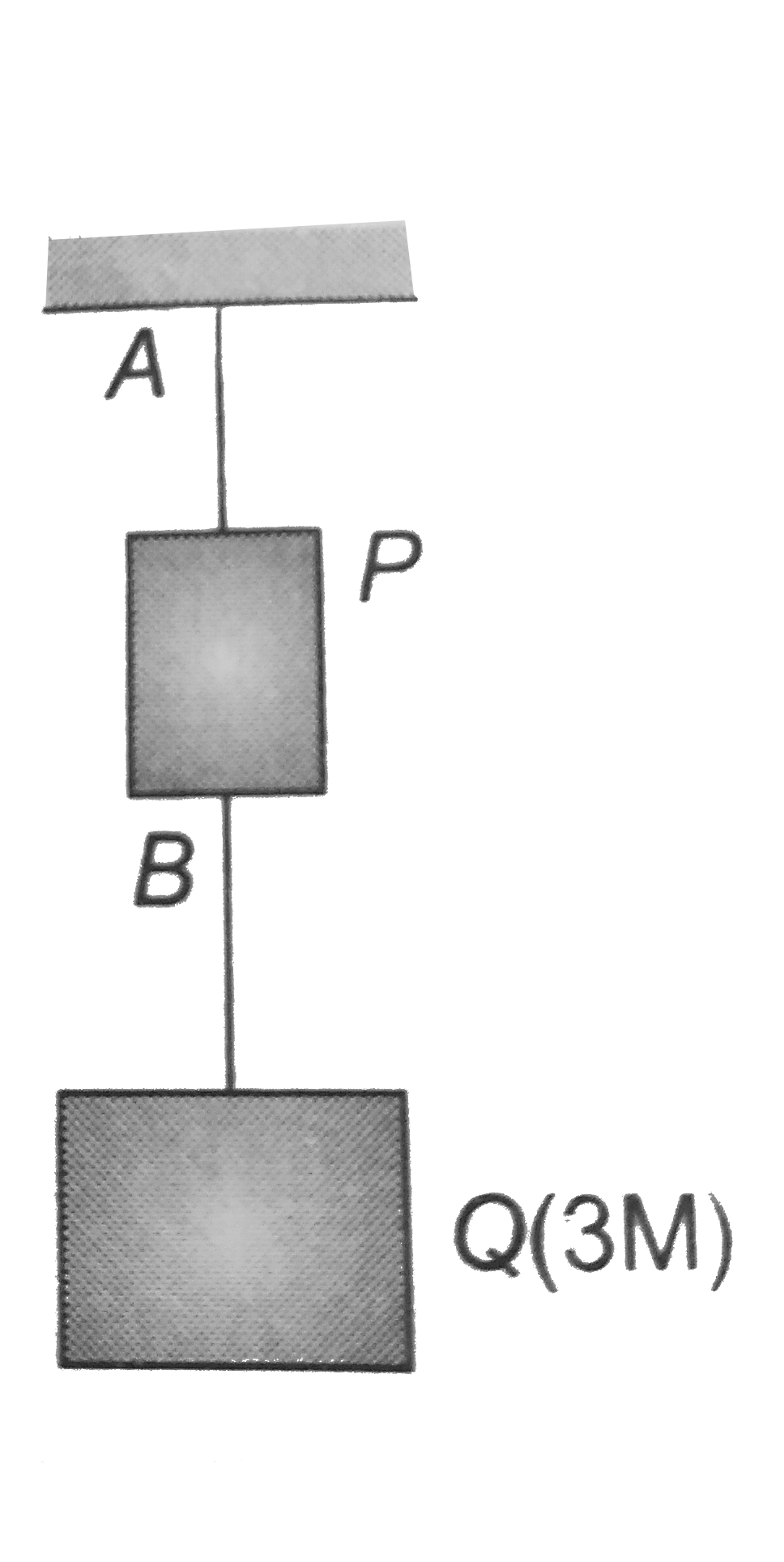
Question 3 - Select One

Wires A and B are connected with blocks P and Q, as shown, the ratio of lengths radii and Young's modulus of wires A and B are r, 2r and 3r respectively (r is a constant). Find the mass of block P if ratio of increase in their corresponding length is $\frac{1}{6 r^{2}}$ . The mass of the block Q is 3M
AM
B3M
C6M
D9M

RESONANCE-DAILY PRACTICE PROBLEMS-dpp 89 illustration

Home
Ask Doubt
Profile