_S01_038_Q01.png)
As per the shown figure the central solid cylinder starts with initial angular velocity ω0 Find the time after which the angular velocity becomes half.
The correct Answer is:t=m(R2−R1)/ln24πηlnaR1
F=ηAdvdz, where dvdz=ωR1−0R2−R1
F=η2πR1lωR1R1−R1

and τ=FR1=2πηR31ωlR2−R1
I∝2πηR31ωlR2−R1
⇒MR212(−dωdt)=2πηR31ωlR2−R1
or −ω0/2∫ω0dωω=4πηR1lm(R2−R1)t∫0dt
⇒t=m(R2−R1)ln24πηlR1

h=40×10−2100−[η=10−1poise =10−2N−sec−m2]
=4×10−3m=4mm
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 89 illustration
Explore 5 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 90 Illustration
Explore 2 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 88
Explore 7 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 54 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCEChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
A uniform rod PQ of length I and mass m is placed on a smooth horizontal surface. It is hinged at one of its ends and touches the conducting circular loop at another end. The system is subjected to vertical magnetic field B0. Rod is given angular velocity ω0 about the axis passing through P. If the time after which its angular velocity becomes half is abmRln2B2t2 . Find the value of (a+b), where a and b are smallest positive integers.

View Solution
The assembly of two discs as shown in figure is placed on a rough horizontal surface and the front disc is given an initial angular velocity ω0. Determine the final linear and angular velocity when both the discs start rolling. it is given that friction is sufficient to sustain rolling the rear wheel from the starting of motion.
View Solution
Knowledge Check
A rod is rotating with angular velocity ω about axis AB. Find cosθ.
 Ag2lω2Bglω2C2g(lω)2D3g2lω2
Ag2lω2Bglω2C2g(lω)2D3g2lω2A solid spherical ball of radius R collides with a rough horizontal surface as shown in figure. At the time of collision its velocity is v0 at an angle θ to the horizontal and angular velocity ω0 as shown . After collision, the angular velocity of ball may
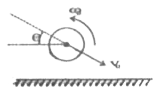 AdecraseBincreaseCremains constantDnone of these
AdecraseBincreaseCremains constantDnone of theseA mass is supported on a frictionless horizontal surface. It Is attached to a string and rotates about a fixed center at an angular velocity ω0.If the length of the string and angular velocity both are doubled, the tension in the string which was initially T0 is now
AT0BT0/2C4T0D8T0
Consider the situation of previous example. If the platform is rotating intially with angular velocity ω0 and then person jumps off tangentially. Determine the new angular velocity of the platform.
View SolutionTwo cylinders having radiii R1 and R2 and rotational inertia I1 and I2 respectively, are supported by fixed axes perpendicular to the plane of figure-5.52. The large cylinder is initially rotating with angular velocityω0. The small cylinder is moved to the right until it touches the large cylinder and is caused to rotate by the frictional force between the two. Eventually, slipping ceases, and the two cylinders rotate at constant rates in opposite directions, (a) Find the final angular velocity ω2 of the small cylinder in terms of I1,I2,R1,R2 and ω0. (b) Is total angular momentum conserved in this case ?
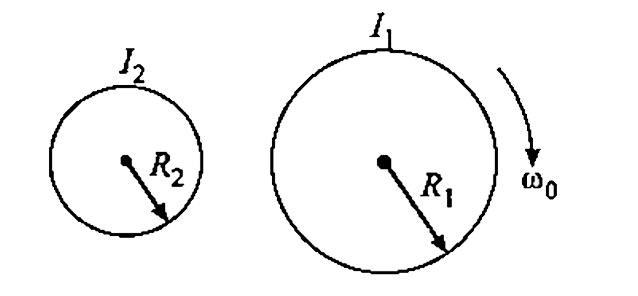
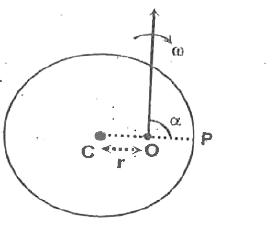
View SolutionRing is fixed on the horizontal surface and a rod starts rotatiing with constant angular velocity ω fixed at O as shown in the figure. Find the magnitude of velocity of intersection points of rod and ring when aplha become 90∘
View SolutionA satellite of mass m revolves around the earth of mass M in a circular orbit of radius r, with an angular velocity ω. If raduis of the orbit becomes 9r, then angular velocity of this orbit becomes
View SolutionA mass attached to a string rotates about a fixed centre with an angular velocity ω in a horizontal plane ,The length of the string and the angular velocity are now doubled .IF T0 is the initial tension in the string , then the new tension will be
View Solution

