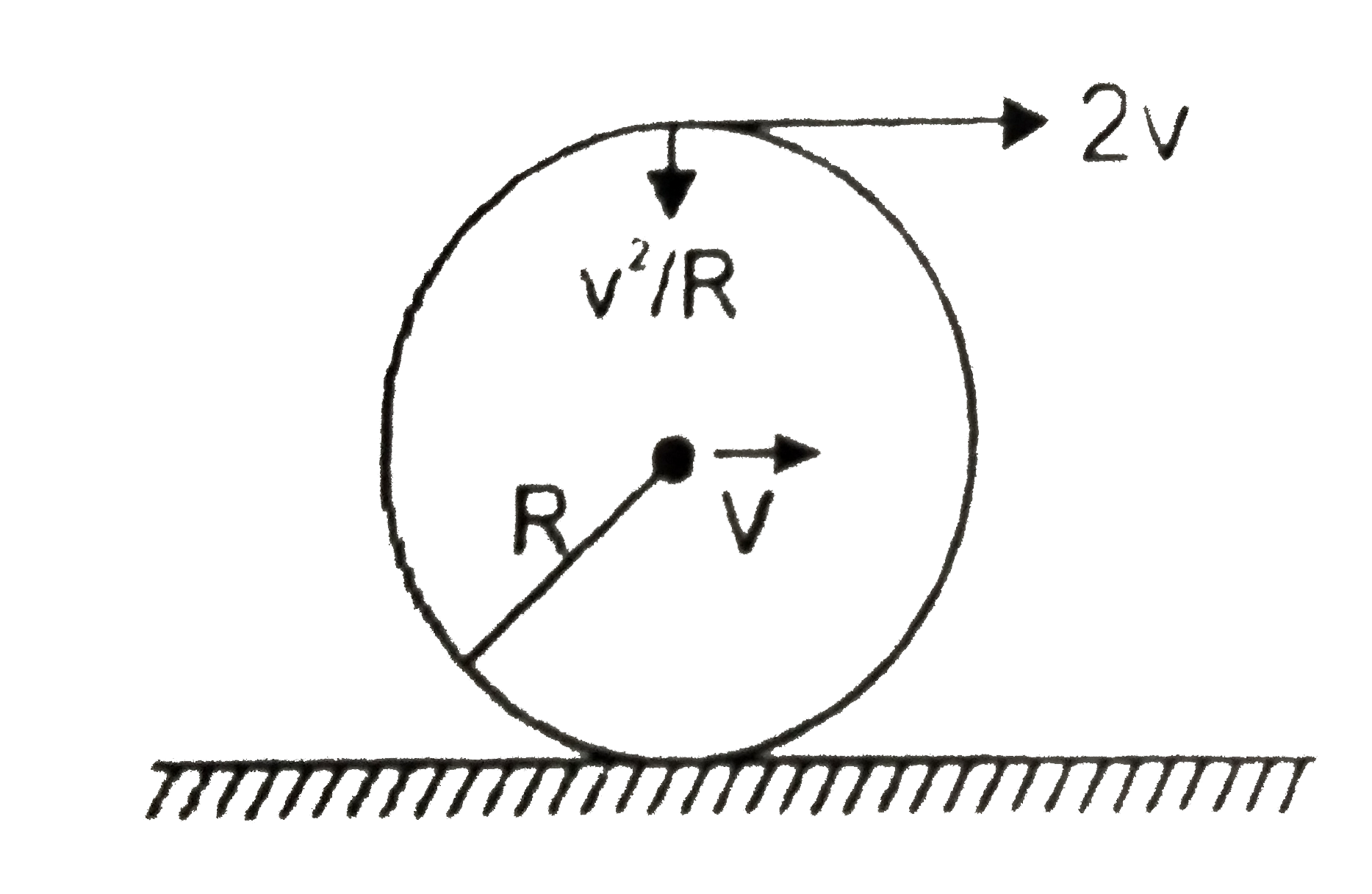
A ring of radius R rolls without slipping on a rough horizontal surface with a constant velocity. The radius of curvature of the path followed by any particle of the ring at the highest point of its path will be :
 .
.
3R
2R
4R
none of these
The correct Answer is:C
Radius of Curvature =(velocity)2No rmalAccel eration=(2v)2v2/R=4R
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 72
Explore 4 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp73
Explore 4 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 70
Explore 7 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 54 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCEChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
A wheel of radius R is rolling without sliding uniformly on a horizontal surface. Find the radius of curvature of the path of a point on its circumference when it is at highest point in its path.
View SolutionA circular disc of radius R rolls without slipping along the horizontal surface with constant velocity v0. We consider a point A on the surface of the disc. Then the acceleration of the point A is:
View Solution
Knowledge Check
The radius of curvature of the path of a charged particle moving in a static uniform magnetic field is
ADirectly propotional to the magnitude of the charge on the particleBDirectly propotional to the magnitude of the liner momentum of the particleCDirectly proportional to the kinetic energy of the particleDInversely proportional to the magnitude of the magnetic fieldThe radius of curvature of the path of a charged particle moving in a static uniform magnetic field is
ADirectly proportional to the magnitude of the charge on the particleBDirectly proportional to the magnitude of the linear momentum of the particleCDirectly proportional to the kinetic energy of the particleDInversely proportional to the magnitude of the magnetic fieldA ring and a disc of same mass roll without slipping along a horizontal surface with same velocity. If the K.E. of ring is 8J, then that of disc is
A2JB4JC6JD16J
A circular disc of radius R rolls without slipping along the horizontal surface with constant velocity v0. We consider a point A on the surface of the disc. Then the acceleration of the point A is:
View SolutionA circular disc of radius R rolls without slipping along the horizontal surface with constant velocity v0 . We consider a point A on the surface of the disc. Then, the acceleration of point A is
View SolutionA solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that vc.m.=v0.
View SolutionA wheel rolls without slipping on a horizontal surface such that its velocity of center of mass is v. The velocity of a particle at the highest point of the rim is
View SolutionA uniform thin ring of mass 0.4kg rolls without slipping on a horizontal surface with a linear velocity of 10 cm/s. The kinetic energy of the ring is
View Solution

