Two stones are projected simultaneously from a tower a differenct angles of projection with same speed 'u'. The distance between two stones is increasing at constant rate 'u'. Then the angle between the initial velocity vectors of the two stones is :
30∘
60∘
45∘
90∘
The correct Answer is:B
To an observer who starts falling freely under gravity from rest at the instant stones are projected, the motion of ston A and B is seen as
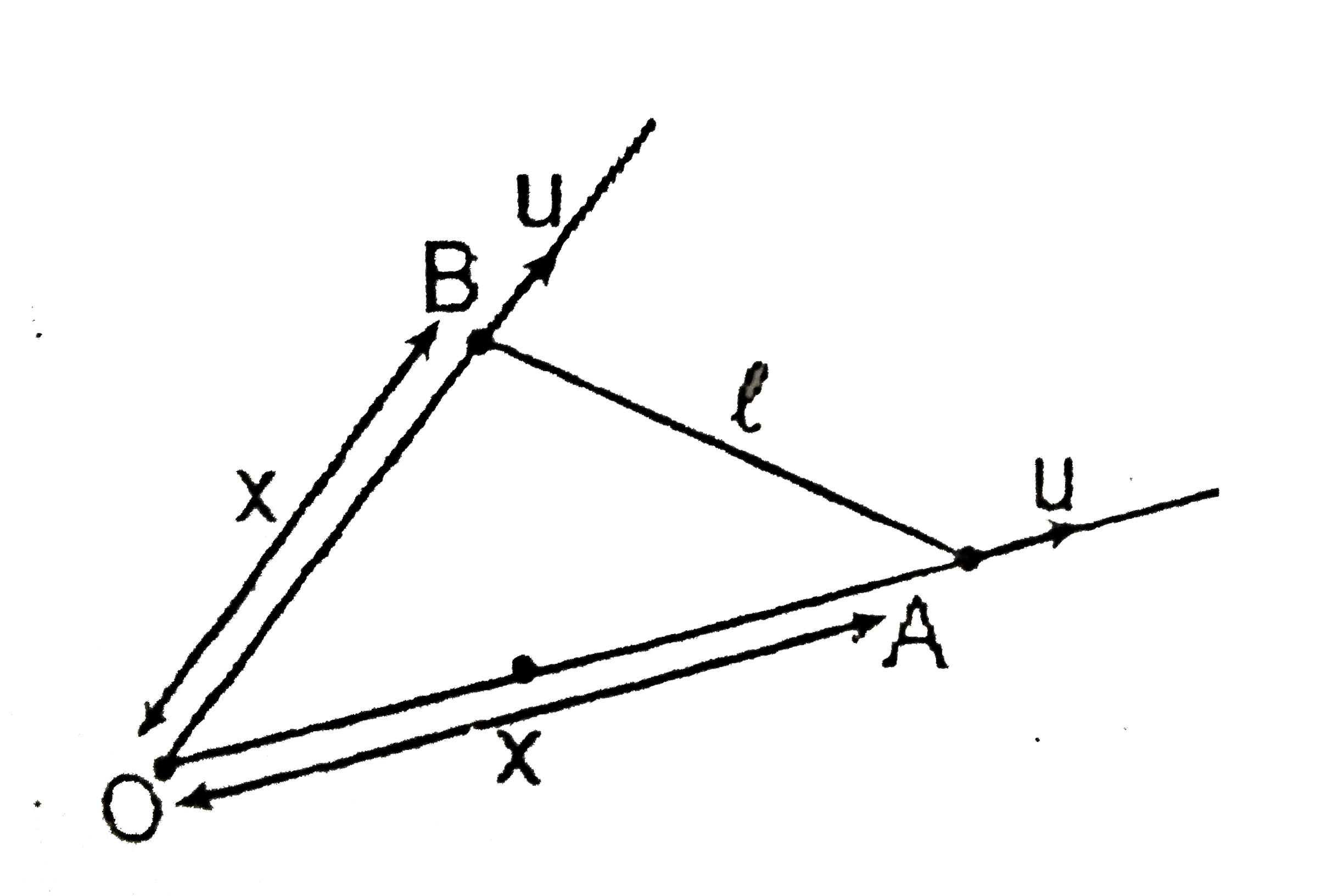
dxdt=u....(1)
dldt=u....(2)
∴x=l and ∠BOA=60∘
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 34
Explore 5 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:DPP 35
Explore 5 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 32
Explore 8 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 54 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCEChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
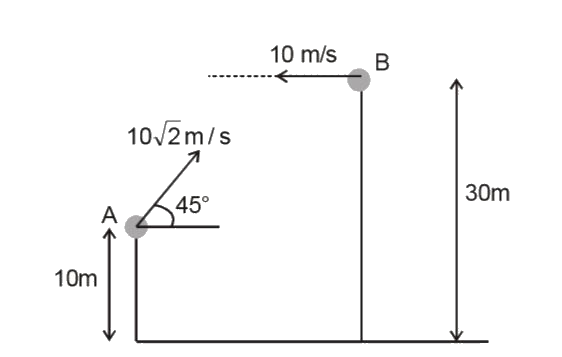
Two projectiles are projected simultaneously from two towers as shwon in figure. If the projectiles collide in the air, then find the distance "s" between the towers.
View SolutionA ball is projected from a point at two different angles with the same speed U and land at the same point in both the cases
View Solution
Knowledge Check
Statement-1: Two stones were projected simultaneously from same point with same speed at different angles from horizontal as shown. They may collide at the point of intersection of their paths.
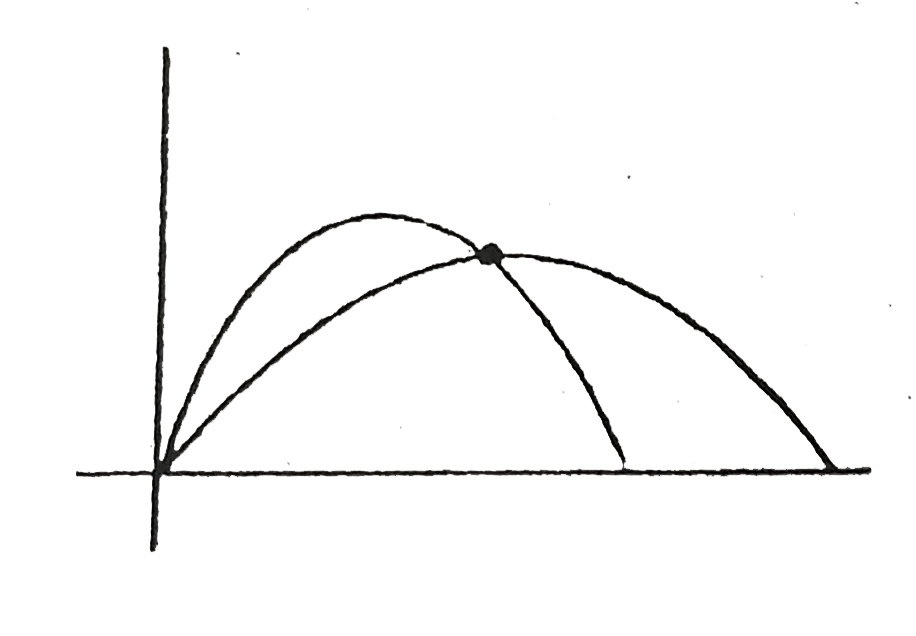
Statement-2: For two particles to collide they must be at the same point in space simultaneously.AStatement -1 is true, statement-2 is true and statement-2 is correct explanation for statement-1.BStatement -1 is true, statement-2 is true and statement-2 is NOT the correct explanation for statement -1.CStatement -1 is true, statement-2 is false.DStatement-1 is false, statement-2 is true.Two stones are thrown up simultaneously from the edge of a cliff with initial speed vand2v. The relative position of the second stone with respect to first varies with time till both the stones strike the ground as.
AlinearlyBfirst linearly then parabolicallyCparabolicallyDfirst parabolically then linearly
(assume that the first stone comes to rest after striking the ground).Two stones are thrown from the top of a tower, one straight down with an initial speed u and the second straight up with the same speed u. When the two stones hit the ground they will have speeds in the ratio.
A2:3B2:1C1:2D1:1
Three stones are projected simultaneously with same speed u from the top of a tower. Stone 1 is projected horizontally and stone 2 and stone 3 are projected making an angle q with the horizontal as shown in fig. Before stone 3 hits the ground, the distance between 1 and 2 was found to increase at a constant rate u.
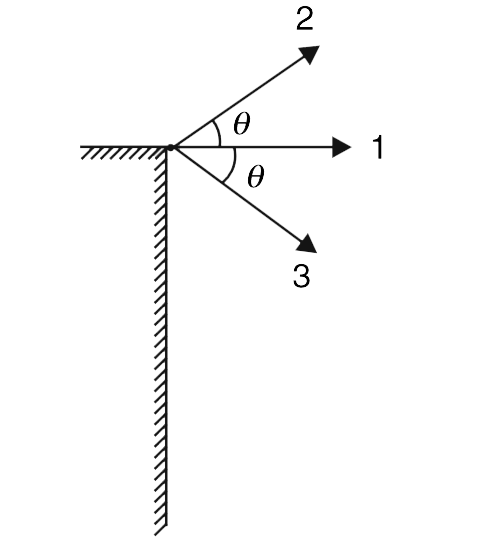
(a) Find θ
(b) Find the rate at which the distance between 2 and 3 increases.
View SolutionTwo stones AandB are projected simultaneously from the top of a 100−m high tower. Stone B is projected horizontally with speed 10ms−1, and stone A is droppd from the tower. Find out the following :
(a) Time of flight of the two stone
(b) Distance between two stones after 3s
(c ) Angle of strike with ground
(d) Horizontal range of particle B.
View SolutionTwo particles are thrown with same initial speed from the same point with angles of projection420 and 480. Find relation between ranges and heights.
View SolutionTwo balls are projected simultaneously from the top of a tall building. The first ball is projected horizontally at speed u1=10m/s and the other one is projected at an angle θ=tan−1(43) to the horizontal with a velocity u2.[g=10m/s2]

(a) Find minimum value of u2(=u0) so that the velocity vector of the two balls can get perpendicular to each other at some point of time during their course of flight. ltbr? (b) Find the time after which velocities of the two balls become perpendicular if the second one was projected with speed u0.
View SolutionA stone is projected with speed u and angle of projection is θ. Find radius of curvature at t=0.
View Solution

