A 1kg block 'B' rests as shown on a bracket 'A' of same mass. Constant forces F1=20N and F2=8N start to act at time t=0 when the distance of block B from pulley is 50cm. Time when block B reaches the pulley is …………………… .( Assume that friction is absent every where. Pulley and string are light.

The correct Answer is:0.5sec
F.B.D. of A.w.r.t. grivel

F1−2F2=mAaA
⇒2−−2×8=1aA
⇒aA=4m/s2
F.B.D. of Bw.r.t.A
So F2−maA=ma2
⇒8−1×4=1aBA=aBA=4m/s2
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 28
7 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp29
5 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 26
8 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
54 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
The velocities of A and B shown in fig. Find the speed (in ms−1) of block C. (Assume that the pulleys and string are ideal).

View SolutionA constant force F=20N acts on a block of mass 2kg which is connected to two blocks of masses m1=1.0kg and m2=2kg as shown in Calculate the accelerations produced in ball the three blocks Assume pulleys are frictionless and weightless
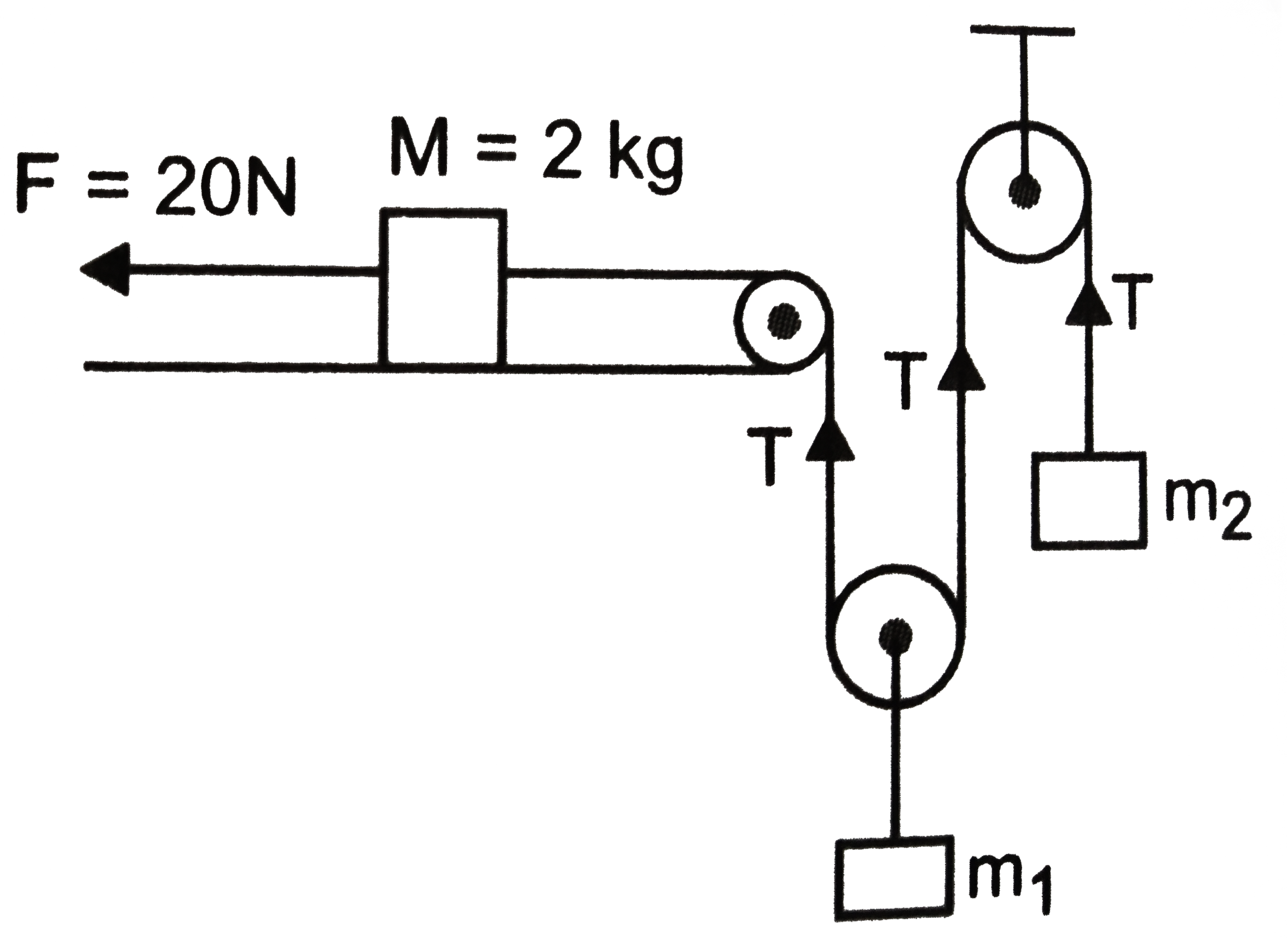 .
.
View Solution
Knowledge Check
In the system shown in figure mB=4kg , and mA=2kg . The pulleys are massless and friction is absent everywhere. The acceleration of block A is.
 A10/3m/s2B20/3m/s2C2m/s2D4m/s2
A10/3m/s2B20/3m/s2C2m/s2D4m/s2Blocks m1 and m2 starts from rest and move to right with accelerations as shown. If t is in second then the time when block m3 again come to rest from t=0 is (pulley and strings are ideal) :
 .A√52secB1+√52secC1+√32secD1sec
.A√52secB1+√52secC1+√32secD1sec
A block B is placed over a cart which in turn lies over a smooth horizontal floor. Block A and Block C are connected to block B with light inextensible strings passing over light frictionless pulleys fixed to the cart as shown. Initially the blocks and the cart are at rest. All the three blocks have mass m and the cart has mass M(M=3m). Now a constant horizontal force of magnitude F is applied to block A towards right.
Q. Let the coefficient of friction between block B and cart is μ(μ>0) and friction is absent everywhere else. Then the maximum value of force F applied to block A such that there is no relative acceleration between block B and cart isAμmgB2μmgC3μmgD4μmg
shown, both blocks are released room rest. Length of 4kg block is 2m and of 1kg is 4m. Find the time they take to cross each other Assume pulley to be light and string to be light and inelastic
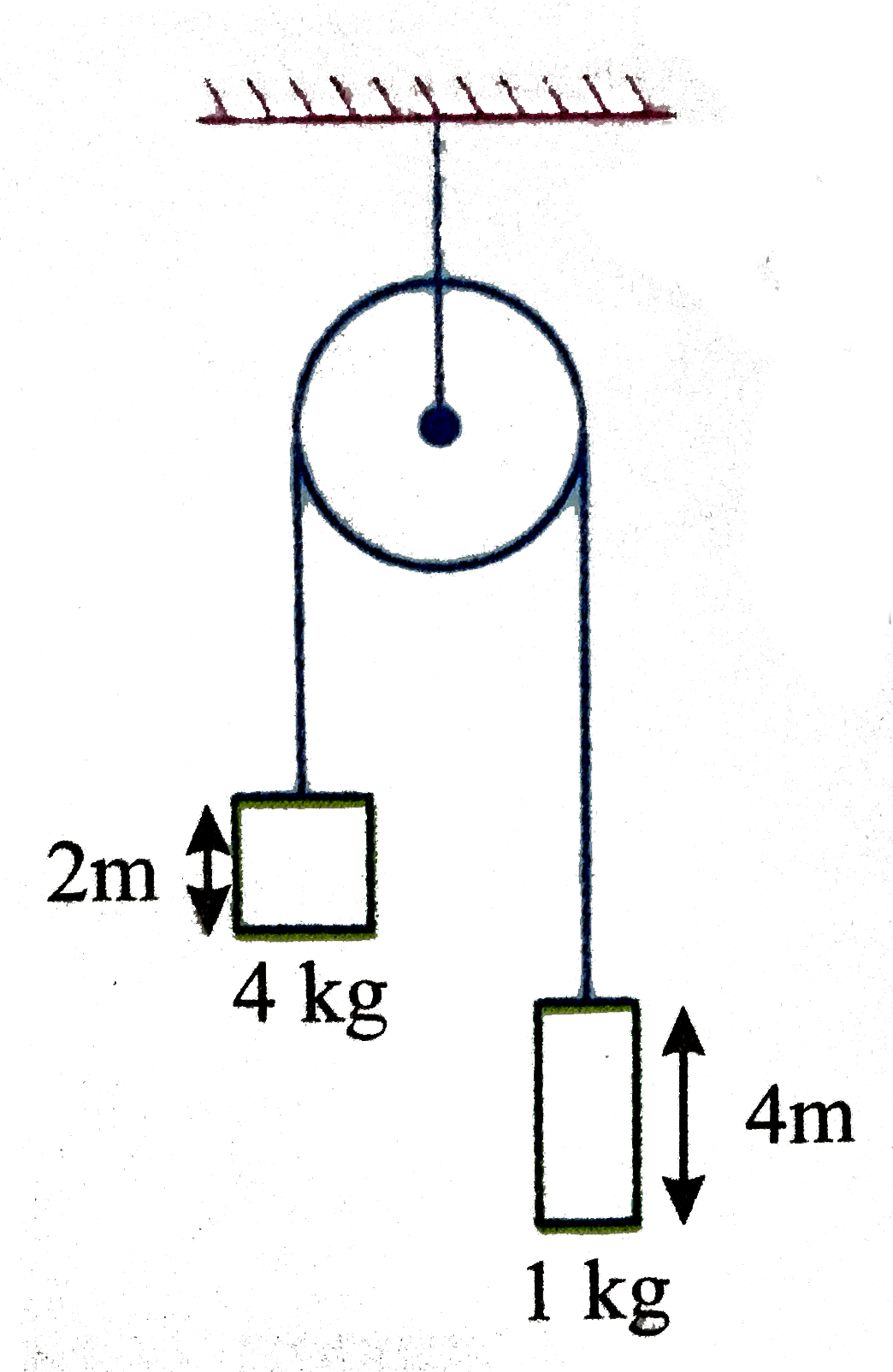 .
.
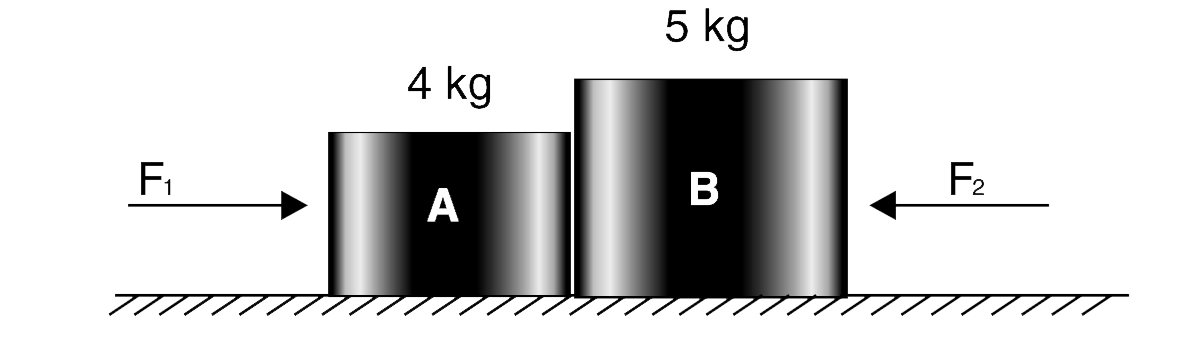
View SolutionTwo rectangular blocks A and B are placed on a horizontal surface at a very small separation. The masses of the blocks are mA=4 kg and mB=5 kg. Coefficient of friction between the horizontal surface and both the blocks is μ=0.4. Horizontal forces F1 and F2 are applied on the blocks as shown. Both the forces vary with time as F1=15+0.5t
F2=2t
Where ‘t’ is time in second.
Plot the variation of friction force acting on the two blocks (fAandfB) vs time till the motion starts. Take rightward direction to be positive for B and leftward direction to be positive forfA.
View SolutionIn the figure shown, all surfaces are smooth and the pulley is massless. A constant force of magnitude F=mg2 is acting on the block of mass M. The acceleration of the block M is :

View SolutionFor the given figure the acceleration of 1 kg block if string is massless and mass of pulley is 2 kg and diameter of pulley is 0.2 m :-
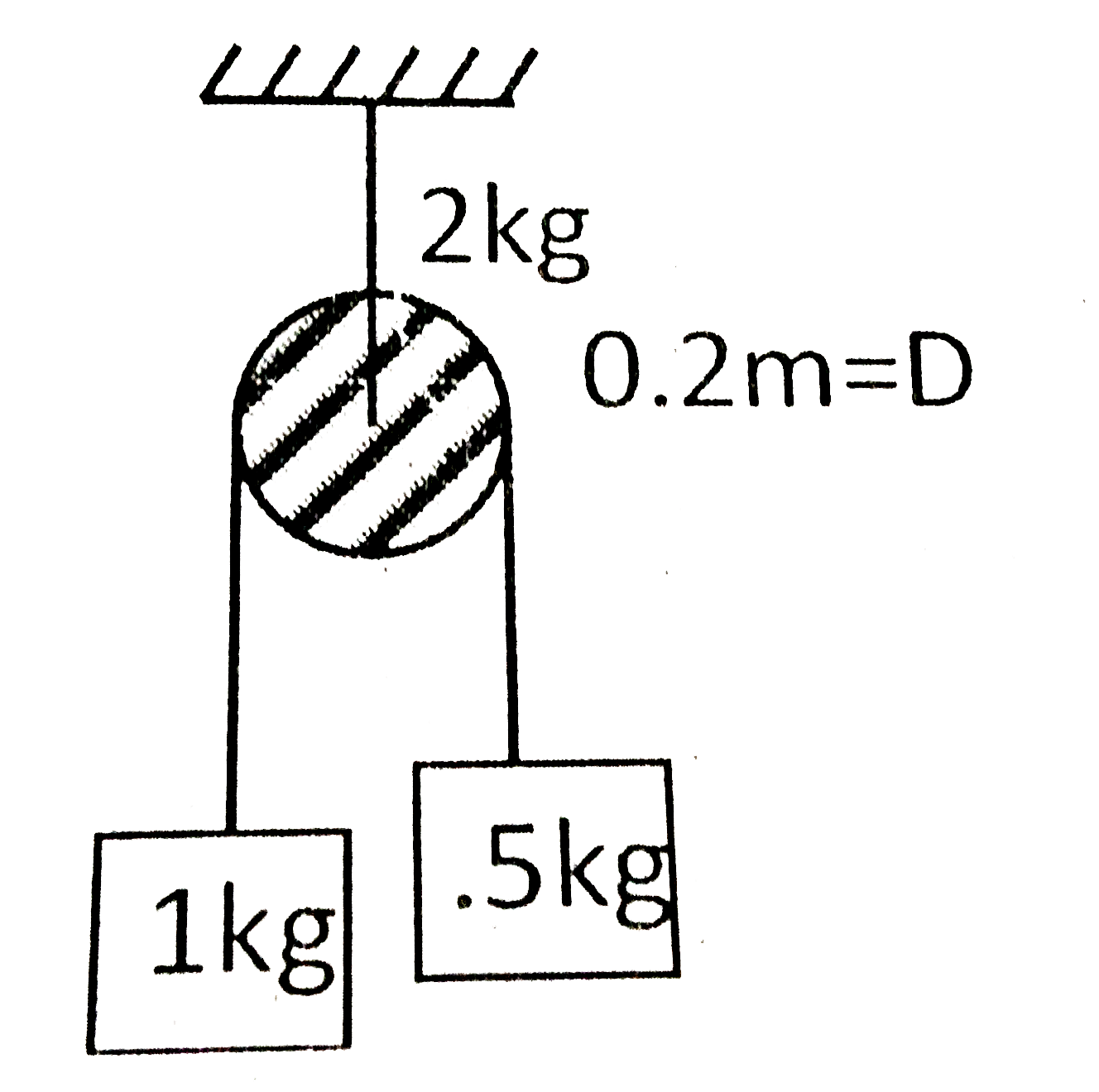
View Solution
A block B is placed over a cart which in turn lies over a smooth horizontal floor. Block A and Block C are connected to block B with light inextensible strings passing over light frictionless pulleys fixed to the cart as shown. Initially the blocks and the cart are at rest. All the three blocks have mass m and the cart has mass M(M=3m). Now a constant horizontal force of magnitude F is applied to block A towards right.
Q. Taking friction to be absent every where the magnitude of tension in the string connecting block B and block C is
View Solution