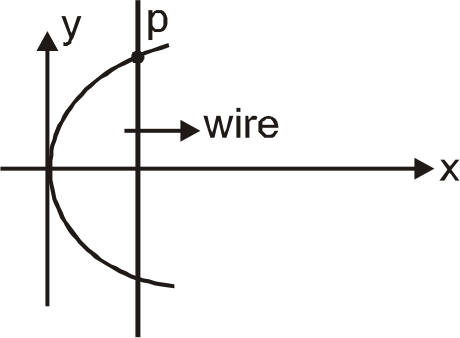
A wire is bent in a parabolic shape followed by equation x=4y2 consider origin as vertex of parabola a wire parallel toy axis moves with constant speed 4m/s along x-axis in the plane of bent wire. Then the acceleration of touching point of straight wire and parabolic wire is (when straight wire has x coordinates =4m)
12ˆi
−14ˆj
2ˆj
4ˆi
The correct Answer is:B
x=4y2
dxdt=8ydydt
Vx=8yVy
Vx=4
ax=0
0=ax=8[y,ay+V2y]−yay=V2y
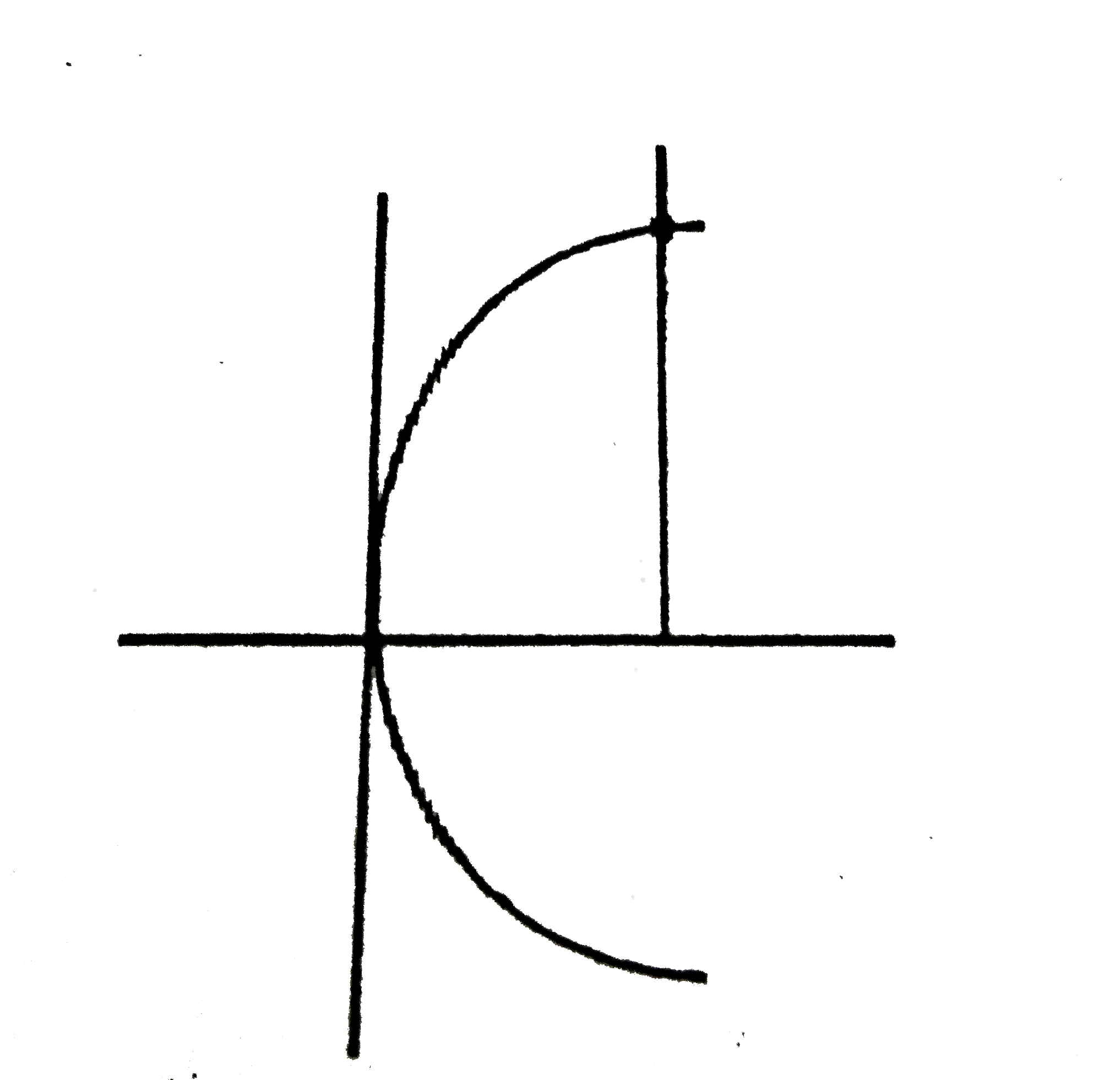
∣∣ay∣∣=v2yy
∣∣ay∣∣=v2x64y3=1664×y3
at y=1⇒∣∣ay∣∣=14
y=1⇒∣∣ay∣∣=14
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:TRUE/FALSE
Explore 2 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 25
Explore 5 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp23
Explore 8 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 54 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCEChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
A thin uniform wire of mass m and length l is bent into to shape of a semicircle. The moment of inertia of that wire about an axis passing through its free ends is
View SolutionA rod of length l is kept parallel to a long wire carrying constant current i . It is moving away from the wire with a velocity v.F∈dtheemf∈duced∈thewirewhenitsdistance∈thewirewhenitsdistanceomthelongwireisx.
View Solution
Knowledge Check
A straight metallic wire of length 1m, is moving normally across a field of 0.1 T with a speed of 10m/s. What is the e.m.f. Induced between the ends of the wire?
A0.5 VB0.75 VC1 VD2 VA piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
AagkBa2gkC2agkDa4gkAngular velocity of smooth parabolic wire y = 4c(x^2) about axis of parabola in vertical plane if bead of mass m does not slip at (a,b) will be
 A√2gcB2√2gcbC2√2gcabD2√2gc
A√2gcB2√2gcbC2√2gcabD2√2gc
A long, straight wire carries a current along the z-axis. One can find two points in the x-y plane such that
View SolutionTwo long, straight wires, one above the other, are separated by a distance 2a and are parallel to the x-axis. Let the y-axis be in the plane of the wires in the direction form the lower wire to the upper wire. Each wire carries current I in the +x-direction. What are the magnitude and direction of the net magnetic field of the two wires at a point in the plane of wires:
(a) midway between them?
(b) at a distance a above the upper wire?
(c) at a distance a below the lower wire?
View SolutionAn infinitely long wire carrying current I is bent to from a L shaped wire. Let the bend be the origin and the two arms be along x and y direction (see figure). Calculate the magnitude of magnetic field at point P (in first quadrant) whose co-ordinates are (x, y).

View SolutionA conducting wire is bent into a loop as shown in the figure. The segment AOB is parabolic given by the equation y2=2x while segment BA is a straight line parallel to the y-axis. The magnetic field in the region is →B−8ˆk and the current in the wire is 2A.
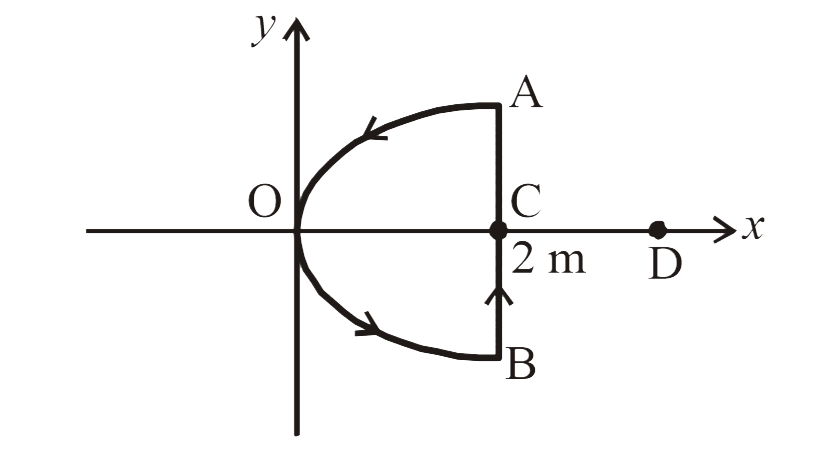
The field created by the current in the loop at point C will be
View SolutionA bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equastion is x2=4ay. The wire frame is fixed and the bead is released from the point y=4a on the wire frame from rest. The tangential acceleration of the bead when it reaches the position given by y=a is

View Solution

