A particle is projected from a horizontal floor with speed 10ms at an angle 30∘ with the floor and striking the floor after sometime. State which is correct.
Velocity of particle will be perpendicular to initial direction two seconds after projection.
Minimum speed of particle will be 5m/sec.
Displecement of particle after half second will be 35/4m.
None of these
The correct Answer is:D
For A
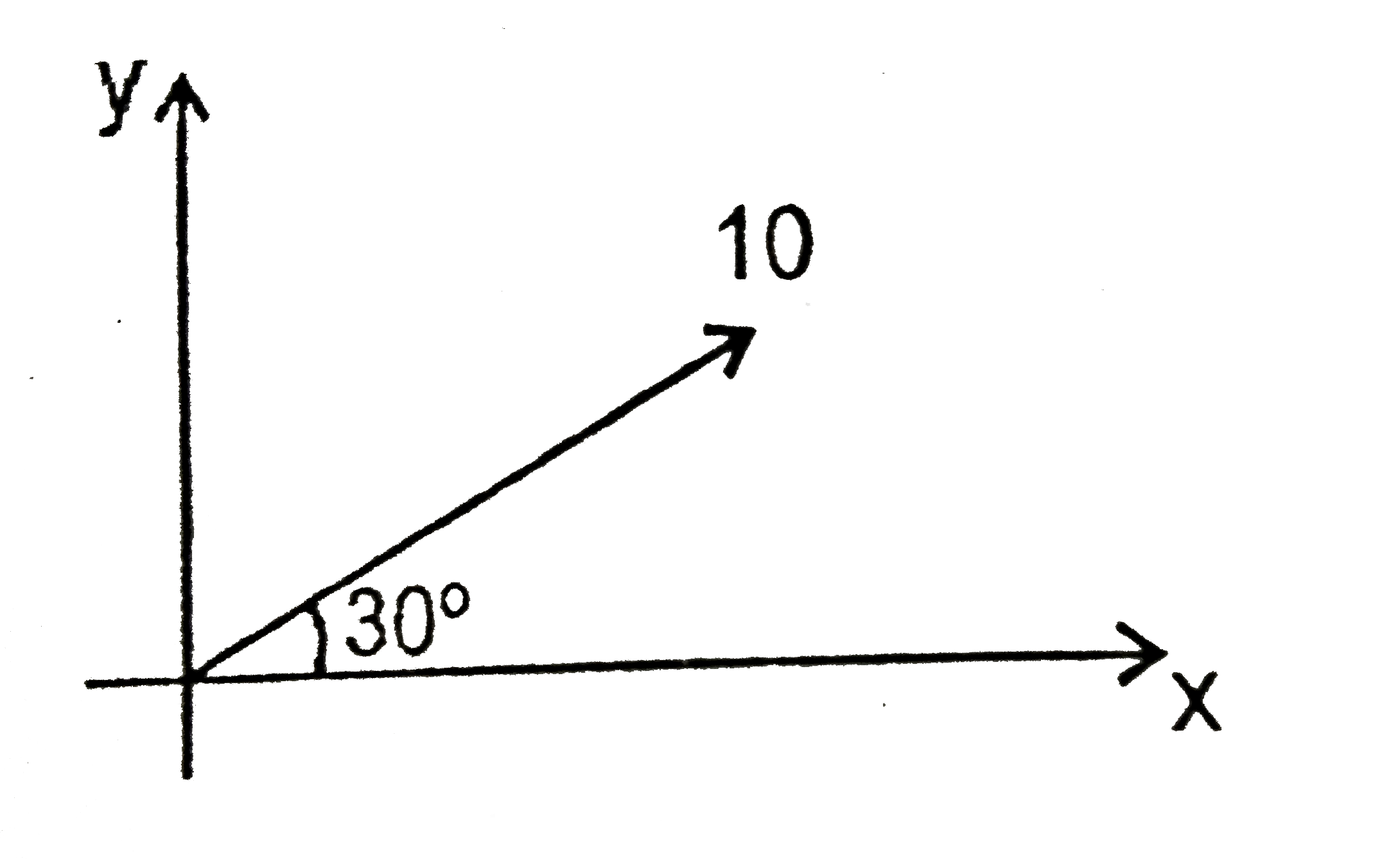
Velocity of the particle will be particular to the initial direction when 10−gsin30∘t=0
∴T=2s,
but total time of flight =2usin30∘g=1s.
So not possible
For B
Minimum speed during the motion is
=ucos30∘=10×√32=5√3m/s
For B
t=12 second
∴particle is at highest point.
Where, displacement =√R24+H2=5√34m
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 16 physics8videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 177videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - DPP NO. 14 PHYSICS10videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise54videos
CURRENT ELECTRICITY
- BOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
A ball is projected from a point on the floor wilth a speed of 15 m/s at an angle of 600 with the horizontal. Will ilt hit a vertical wall 5 m away from the point of projection and perpendiculaer to the plane of projection without and perpendicular to the plane of projection without hitting the floor? will the answer differ if the wall is 22 m away?
View SolutionA ball is projected from the floor of a cabin of height 7m with speed 20 m/s at an angle of 37∘ with the floor of cabin. It makes a successive collision with the wall of cabin and then return again to its floor. Assume all collisions are perfectly elastic. Find time taken (in sec) by the ball to reach the floor after collisions with the ceiling of cabin.
View Solution
Knowledge Check
- Question 1 - Select One
A particle is projected with speed 10m/s at angle 60∘ with the horizontal. Then the time after which its speed becomes half of initial.
A12 secB1 secC√3/2secD√3/2sec - Question 2 - Select One
A particle strikes a horizontal frictionless floor with a speed u at an angle θ with the vertical, and rebounds with a speed v at an angle ϕ with vertical. The coefficient of restitution between the particle and floor is e. The angle ϕ is equal to
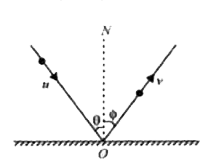 AθB(1+e)θCtan−1(etanθ)Dtan−1(1etanθ)
AθB(1+e)θCtan−1(etanθ)Dtan−1(1etanθ) - Question 3 - Select One
A particle strikes a horizontal frictionless floor with a speed u at an angle θ with the vertical, and rebounds with a speed v at an angle ϕ with vertical. The coefficient of restitution between the particle and floor is e. The magnitude of v is
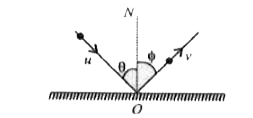 AeuB(1−e)uCu√e2sin2θ+cos2θDu√sin2θ+e2cos2θ
AeuB(1−e)uCu√e2sin2θ+cos2θDu√sin2θ+e2cos2θ
A particle A is projected with an initial velocity of 60 m/s. at an angle 30∘ to the horizontal. At the same time a second particle B is projected in opposite direction with initial speed of 50 m/s from a point at a distance of 100 m from A. If the particles collide in air, find (a) the angle of projection ∝ of particle B,
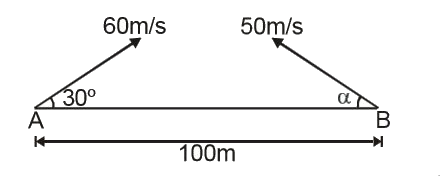 View Solution
View SolutionA particle is projected with a velocity 10 m//s at an angle 37∘ to the horizontal. Find the location at which the particle is at a height 1 m from point of projection.
View SolutionA particle strikes a horizontal smooth floor with a velocity a making an angle θ with the floor and rebounds with velocity v making an angle ϕ with the floor. If the coefficient of restitution between the particle and the floor is e, then
View SolutionA particle strikes a horizontal smooth floor with a velocity u making an angle θ with the floor and rebounds with velocity v making an angle ϕ with the floor. The coefficient of restitution between the particle and the floor is e.
View SolutionA particle strikes a horizontal frictionless floor with a speed u, at an angle θ with the vertical, and rebounds with a speed υ, at an angle ϕ with the vertical. The coefficient of restitution between the particle and the floor is e. The angle ϕ is equal to :
 View Solution
View Solution

