A particle moves along x− axis. It's velocity is a function of time according to relation V=(3t2−18t+24)m/s assume at t=0 particle is at origin.
Distance travelled by particle in 0 to 3 second time interval is :
18m
20m
22m
24m
The correct Answer is:C
V=(3t2−18t+24)m/s
V=3(t−2)(t−4)
s=∣∣
∣∣2∫0Vdt∣∣
∣∣+∣∣
∣∣3∫2Vdt∣∣
∣∣
=∣∣
∣∣2∫0(3t2−18t+24)dt∣∣
∣∣+∣∣
∣∣3∫2(3t2−18t+24)dt∣∣
∣∣=|20|+|−2|=22m
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - Dpp no 12 Physics
8 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - Dpp no. 13 physics
5 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - Dpp no 11 physics
6 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
54 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
A particle moves along a straight line.The acceleration of the particle as function of time is given by a=6t−12 .Initial velocity of particle is 9ms .Find distance (in meters) travelled by particle in 4 seconds.
View SolutionA particle is moving along x-axis such that its velocity varies with time according to v=(3m/s2)t−(2m/s3)t2. Find the velocity at t = 1 s and average velocity of the particle for the interval t = 0 to t = 5 s.
View Solution
Knowledge Check
A particle moves along x− axis. It's velocity is a function of time according to relation V=(3t2−18t+24)m/s assume at t=0 particle is at origin.
Time interval in which particle speed continuous decreases?A0−3secB0−2secC2−4secD2−3secA particle moves along x− axis. It's velocity is a function of time according to relation V=(3t2−18t+24)m/s assume at t=0 particle is at origin.
Which of the following graph may be correct for the motion of particleA B
B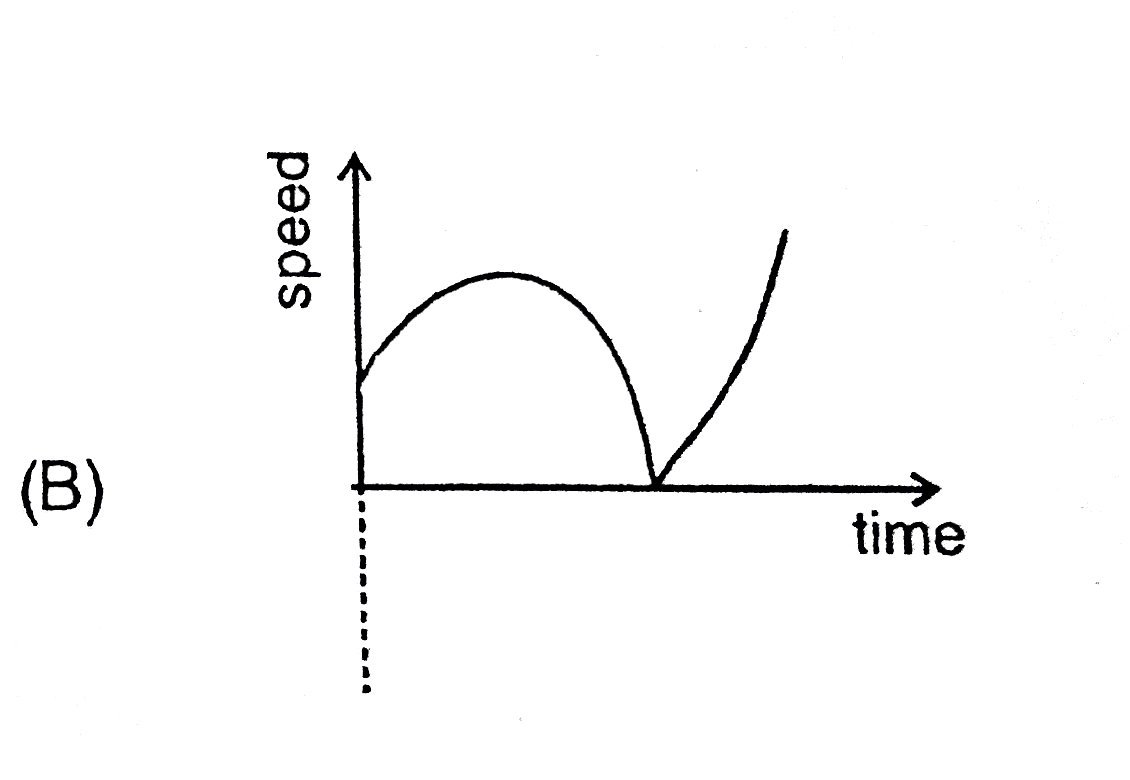 C
C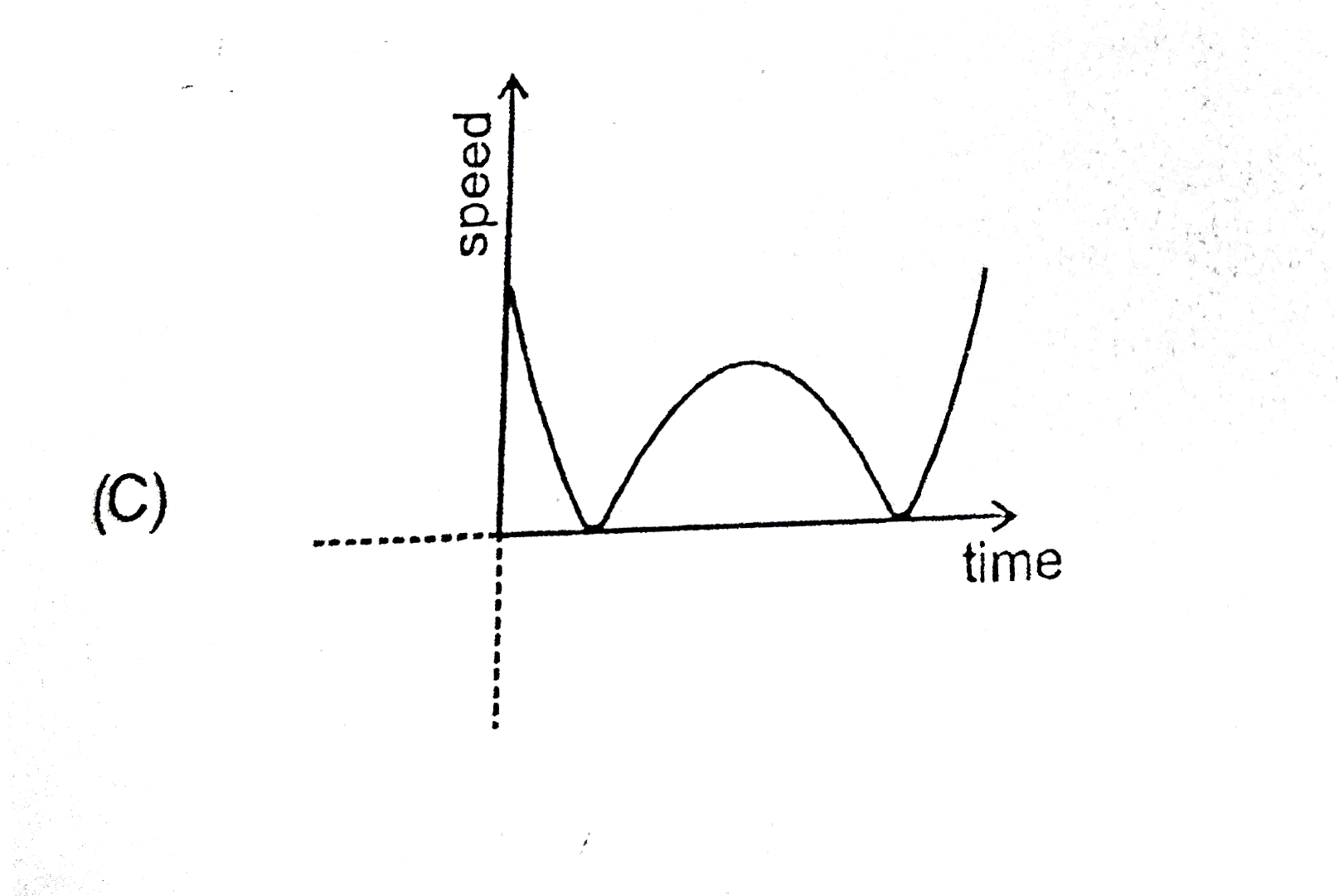 D
D
A particle is moving on a straight line with velocity (v) as a function of time (t) according to relation v=(5t2−3t+2)m/s . Now give the answer of following questions :
Velocity of particle at t = 3 sec. is :A30m/sB38m/sC22m/sD36m/s
A particle is moving on a straight line with velocity (v) as a function of time (t) according to relation v=(5t2−3t+2)m/s . Now give the answer of following questions :
Acceleration of particle at the end of 3rd second of motion is :
View SolutionThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The distance travelled by particle from t=0 to t=2seconds is :
View SolutionThe position of a particle along x-axis at time t is given by x=1+t−t2. The distance travelled by the particle in first 2 seconds is
View SolutionA particle is moving with speed v=b√x along positive x-axis. Calculate the speed of the particle at time t=τ (assume that the particle is at origin at t = 0).
View SolutionA particle is moving along the x-axis whose acceleration is given by a=3x−4, where x is the location of the particle. At t = 0, the particle is at rest at x=4/3m. The distance travelled by the particles in 5 s is
View Solution
