जल से भरे 88 cm गहराई के किसी टैंक की तली (bottom ) पर कोई छोटा बल्ब रखा गया है जल के पृष्ठ का वह क्षेत्र ज्ञात कीजिए जिससे बल्ब का प्रकाश निर्गत हो सकता है। जल का अपवर्तनांक 1.33 है। ( बल्ब को बिंदु प्रकाश-स्त्रोत मान सकते है । )

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

जैसा कि चित्र से स्पष्ट है व्यास AB (= 2R ) के वृत्ताकार क्षेत्र से प्रकाश निर्गत हो सकेगा (उससे बाहर पूर्ण आंतरिक परावर्तन के कारण प्रकाश जल के ऊपरी पृष्ठ से निर्गत नहीं हो पाएगा )।
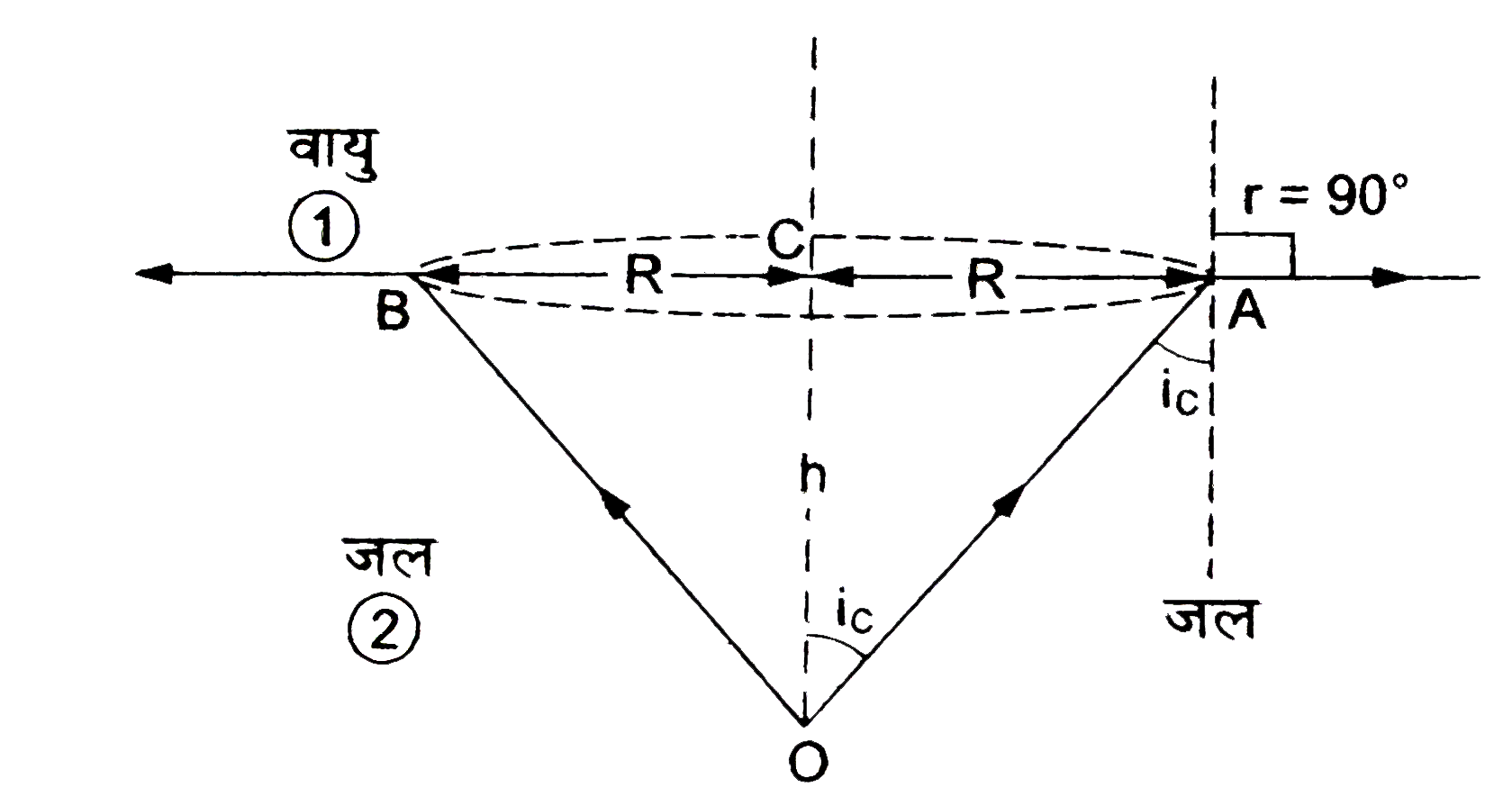
ocr_image
यहाँ i c क्रांतिक-कोण है जिसके संगत का अपवर्तन-कोण r = 90 ∘ .
दिया गया है की जल का अपवर्तनांक a μ w = 1.33 , जल की गहराई h = 88 cm.
सूत्र sin i c = 1 1 μ 2 से,
sin i c = 1 a μ w = 1 1.33 = 0.7519 = sin 48 ∘ 45 ′ .
चित्र की ज्यामिति से,
tan i c = R h
या R = h tan i c = ( 88 c m ) ( tan 48 ∘ 45 ′ )
= 88 c m × 1.1403
= 100 c m = 1 m .
वृत्ताकार क्षेत्र, जिससे प्रकाश निर्गत हो सकता है, का क्षेत्रफल
A = π R 2 = 3.14 × ( 1 m ) 2 = 3.14 m 2 .
विकल्पतः - दिया गया है कि
जल का अपवर्तनांक μ = 1.33 .
जल की गहराई h = 88 c m = 0.88 m
चित्र से , tan i c = R h
∴ R = h tan i c = h sin i c cos i c = h sin i c 1 - sin 2 i c
= h 1 μ 1 - ( 1 μ ) 2 = h μ = 1 μ 2 - 1 μ 2
या R = h μ 2 - 1 = 88 c m ( 1.33 ) 2 - 1 = 88 c m 1.77 - 1
= 88 c m 0.77 = 88 c m 0.88 = 100 c m = 1 m .

Updated on:21/07/2023
|
Class 12PHYSICSGEOMETRICAL OPTICS

Topper's Solved these Questions

Similar Questions